题目内容
17.(1)若$cosθ=\frac{{\sqrt{2}}}{3}$,求$\frac{{sin(θ-5π)cos(θ-\frac{π}{2})cos(8π-θ)}}{{sin(θ-\frac{3π}{2})sin(-θ-4π)}}$的值.(2)求函数$f(x)=lg(2cosx-1)+\sqrt{49-{x^2}}$的定义域.
分析 (1)直接利用诱导公式以及同角三角函数的基本关系式化简求解即可.
(2)通过对数的真数大于0,开偶次方被开方数非负,列出不等式组,然后求出函数的定义域.
解答 解:(1)$cosθ=\frac{{\sqrt{2}}}{3}$,所以$\frac{{sin(θ-5π)cos(θ-\frac{π}{2})cos(8π-θ)}}{{sin(θ-\frac{3π}{2})sin(-θ-4π)}}$
=$\frac{(-sinθ)sinθcosθ}{cosθ(-sinθ)}$
=$sinθ=±\sqrt{1-{cos}^{2}θ}=±\frac{\sqrt{7}}{3}$
(2)由题意可知:$\left\{\begin{array}{l}cosx>\frac{1}{2}\\ 49-{x^2}≥0\end{array}\right.$,
解得:$\left\{{\begin{array}{l}{2kπ-\frac{π}{3}<x<2kπ+\frac{π}{3},k∈Z}\\{-7≤x≤7}\end{array}}\right.$,
得:$-7≤x<-\frac{5π}{3}$或$-\frac{π}{3}<x<\frac{π}{3}$或$\frac{5π}{3}<x≤7$.
故函数的定义域为$\{x|-7≤x<-\frac{5π}{3}或-\frac{π}{3}<x<\frac{π}{3}或\frac{5π}{3}<x≤7\}$.
点评 本题考查三角函数的化简求值,诱导公式以及同角三角函数的基本关系式的应用,函数的定义域的求法,考查计算能力.

练习册系列答案
相关题目
7.设数f(log2x)的定义域是(2,4),则函数$f({\frac{x}{2}})$的定义域是( )
| A. | (2,4) | B. | (2,8) | C. | (8,32) | D. | $(\frac{1}{2},1)$ |
5.已知抛物线y2=4x上的两点A,B满足|AB|=6,则弦AB中点到y轴的最小距离为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
12.函数$y=2sin(2x+\frac{π}{3})$的图象( )
| A. | 关于原点对称 | B. | 关于点($\frac{π}{6}$,0)对称 | ||
| C. | 关于y轴对称 | D. | 关于直线$x=\frac{π}{12}$对称 |
9.已知集合A={x|(x+1)(x-2)≤0},B={x|-2<x<2},则A∩B=( )
| A. | {x|-1≤x≤2} | B. | {x|-1≤x<2} | C. | {x|-1<x<2} | D. | {x|-2<x≤1} |
6.函数y=-cos2x+$\sqrt{3}$cosx+$\frac{5}{4}$,则( )
| A. | 最大值是$\frac{5}{4}$,最小值是1 | B. | 最大值是1,最小值是$\frac{1}{4}$-$\sqrt{3}$ | ||
| C. | 最大值是2,最小值是$\frac{1}{4}$-$\sqrt{3}$ | D. | 最大值是2,最小值是$\frac{5}{4}$ |
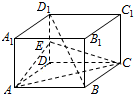 如图,正方体ABCD-A1B1C1D1的棱长为2,E为DD1的中点,
如图,正方体ABCD-A1B1C1D1的棱长为2,E为DD1的中点,