题目内容
 设抛物线C:y2=2px(p>0)的焦点为F,直线l过F且与抛物线C交于M、N两点,已知直线l与x轴垂直时,△OMN的面积为2(O为坐标原点).
设抛物线C:y2=2px(p>0)的焦点为F,直线l过F且与抛物线C交于M、N两点,已知直线l与x轴垂直时,△OMN的面积为2(O为坐标原点).(Ⅰ)求抛物线C的方程;
(Ⅱ)问是否存在直线l,使得以M、N为对角线的正方形的第三个顶点恰好在y轴上,若存在,求直线l的方程;若不存在,说明理由.
考点:直线与圆锥曲线的关系,抛物线的标准方程
专题:综合题,圆锥曲线的定义、性质与方程
分析:(Ⅰ)直线l与x轴垂直时,|MN|=2p,利用△OMN的面积为2,求出p,即可求抛物线C的方程;
(Ⅱ)求出线段MN的垂直平分线,可得P的坐标,利用
•
=0,即可得出结论.
(Ⅱ)求出线段MN的垂直平分线,可得P的坐标,利用
| PM |
| PN |
解答:
解:(Ⅰ)直线l与x轴垂直时,|MN|=2p,
∵△OMN的面积为2,
∴
•2p•
=
=2,
∴p=2,
∴抛物线C的方程为y2=4x;
(Ⅱ)直线l与x轴垂直时,不满足,设正方形的第三个顶点P(0,y0),M(x1,y1),N(x2,y2)
设l:y=k(x-1)(k≠0),代入y2=4x,可得k2x2-(2k2+4)x+k2=0,
∴x1+x2=
,x1x2=1,
∴MN的中点为(
,
),
∴线段MN的垂直平分线为y-
=-
(x-1-
),
∴P(0,
+
),
∵
•
=0,
∴x1x2+(y1-y0)(y2-y0)=0,
∴1-4-y0•
+y02=0,
由y0=
+
代入,可得(3k4-4)(k2+1)=0,
∴k=±
,
∴存在直线l:y=±
(x-1).
∵△OMN的面积为2,
∴
| 1 |
| 2 |
| p |
| 2 |
| p2 |
| 2 |
∴p=2,
∴抛物线C的方程为y2=4x;
(Ⅱ)直线l与x轴垂直时,不满足,设正方形的第三个顶点P(0,y0),M(x1,y1),N(x2,y2)
设l:y=k(x-1)(k≠0),代入y2=4x,可得k2x2-(2k2+4)x+k2=0,
∴x1+x2=
| 2k2+4 |
| k2 |
∴MN的中点为(
| k2+2 |
| k2 |
| 2 |
| k |
∴线段MN的垂直平分线为y-
| 2 |
| k |
| 1 |
| k |
| 2 |
| k2 |
∴P(0,
| 3 |
| k |
| 2 |
| k3 |
∵
| PM |
| PN |
∴x1x2+(y1-y0)(y2-y0)=0,
∴1-4-y0•
| 4 |
| k |
由y0=
| 3 |
| k |
| 2 |
| k3 |
∴k=±
|
∴存在直线l:y=±
|
点评:本题考查抛物线的方程,考查直线与抛物线的位置关系,考查韦达定理的运用,考查学生的计算能力,难度中等.

练习册系列答案
相关题目
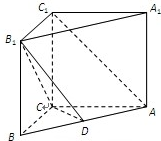 已知直三棱柱ABC-A1B1C1中,AC=BC=AA1=4,AC⊥BC,若D是AB中点.
已知直三棱柱ABC-A1B1C1中,AC=BC=AA1=4,AC⊥BC,若D是AB中点.