题目内容
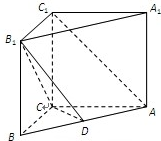 已知直三棱柱ABC-A1B1C1中,AC=BC=AA1=4,AC⊥BC,若D是AB中点.
已知直三棱柱ABC-A1B1C1中,AC=BC=AA1=4,AC⊥BC,若D是AB中点.(Ⅰ)求证:AC1∥平面B1CD;
(Ⅱ)求异面直线AC1和CD所成的角.
考点:异面直线及其所成的角,直线与平面平行的判定
专题:空间角
分析:(Ⅰ)连接BC1交B1C于点E,连结DE,由已知条件推导出DE∥AC1,由此能证明AC1∥平面B1CD.
(Ⅱ)由DE∥AC1,得到∠CDE为异面直线AC1和CD所成的角或其补角,由此能求出异面直线AC1和CD所成的角的大小.
(Ⅱ)由DE∥AC1,得到∠CDE为异面直线AC1和CD所成的角或其补角,由此能求出异面直线AC1和CD所成的角的大小.
解答:
(Ⅰ)证明:连接BC1交B1C于点E,连结DE,
∵ABC-A1B1C1是直三棱柱,
∴三棱柱ABC-A1B1C1的侧面都是矩形,
∴点E是BC1的中点,…(2分)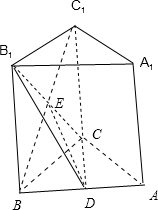
又∵D是AB的中点,
∴DE∥AC1,…(4分)
又∵DE⊆平面B1CD,AC1?平面B1CD,
∴AC1∥平面B1CD.…(7分)
(Ⅱ)解:∵DE∥AC1,
∴∠CDE为异面直线AC1和CD所成的角或其补角,…(8分)
∵AC=BC=AA1=4,三角形ABC是直角三角形,…(8分)
∴AB=4
…(9分)
∴CD=
AB=2
,DE=
AC1=2
,CE=
CB1=2
,
∴三角形CDE是等边三角形,…(12分)
∴∠CDE=
.
∴异面直线AC1和CD所成的角为
.…(13分)
∵ABC-A1B1C1是直三棱柱,
∴三棱柱ABC-A1B1C1的侧面都是矩形,
∴点E是BC1的中点,…(2分)

又∵D是AB的中点,
∴DE∥AC1,…(4分)
又∵DE⊆平面B1CD,AC1?平面B1CD,
∴AC1∥平面B1CD.…(7分)
(Ⅱ)解:∵DE∥AC1,
∴∠CDE为异面直线AC1和CD所成的角或其补角,…(8分)
∵AC=BC=AA1=4,三角形ABC是直角三角形,…(8分)
∴AB=4
| 2 |
∴CD=
| 1 |
| 2 |
| 2 |
| 1 |
| 2 |
| 2 |
| 1 |
| 2 |
| 2 |
∴三角形CDE是等边三角形,…(12分)
∴∠CDE=
| π |
| 3 |
∴异面直线AC1和CD所成的角为
| π |
| 3 |
点评:本题考查直线与平面平行的证明,考查异面直线所成角的大小的求法,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案
相关题目
某曲线y=f(x)在x=5处的切线方程为y=-x+8,则f(5)+f′(5)=( )
| A、6 | B、2 | C、4 | D、-2 |
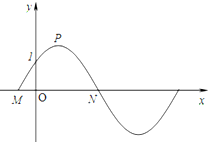 已知如图,函数y=2sin(
已知如图,函数y=2sin(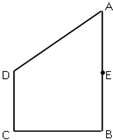 如图所示,在直角梯形ABCD中,E是AB的中点,∠B=∠C=90°,
如图所示,在直角梯形ABCD中,E是AB的中点,∠B=∠C=90°,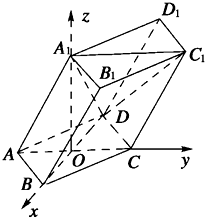 如图,棱柱ABCD-A1B1C1D1的所有棱长都等于2,∠ABC=60°,平面AA1C1C⊥平面ABCD,∠A1AC=60°.
如图,棱柱ABCD-A1B1C1D1的所有棱长都等于2,∠ABC=60°,平面AA1C1C⊥平面ABCD,∠A1AC=60°. 设抛物线C:y2=2px(p>0)的焦点为F,直线l过F且与抛物线C交于M、N两点,已知直线l与x轴垂直时,△OMN的面积为2(O为坐标原点).
设抛物线C:y2=2px(p>0)的焦点为F,直线l过F且与抛物线C交于M、N两点,已知直线l与x轴垂直时,△OMN的面积为2(O为坐标原点). 正方形ABCD的边长为1,AE=1,DE=
正方形ABCD的边长为1,AE=1,DE=