题目内容

设向量
a
，
b
满足|
a
|=|
b
|=1，|3
a
-
b
|=
5
．
（1）求|
a
+3
b
|的值；
（2）求3
a
-
b
与
a
+3
b
夹角的余弦值．
考点：数量积表示两个向量的夹角,向量的模
专题：平面向量及应用
分析：（1）由|3
a
-
b
|=
5
得(3
a
-
b
)2=9
a
2-6
a
•
b
+
b
2=5，求得 
a
•
b
 的值，再根据|
a
+3
b
|=
(
a
+3
b
)2
 计算求得结果．
（2）设3
a
-
b
与
a
+3
b
夹角为θ，先求得（3
a
-
b
）•（
a
+3
b
）的值，再根据cosθ=
(3
a
-
b
)•(
a
+3
b
)
|3
a
-
b
|•|
a
+3
b
|
 计算求得结果．
解答： 解：（1）由|3
a
-
b
|=
5
，得(3
a
-
b
)2=9
a
2-6
a
•
b
+
b
2=5，
因为|
a
|=|
b
|=1，所以
a
•
b
=
5
6
．
∴|
a
+3
b
|=
(
a
+3
b
)2
=
a
2+6
a
•
b
+9
b
2
=
1+5+9
=
15
．
（2）设3
a
-
b
与
a
+3
b
夹角为θ，∵（3
a
-
b
）•（
a
+3
b
）=3
a
2+8
a
•
b
-3
b
2=
20
3
，
则 cosθ=
(3
a
-
b
)•(
a
+3
b
)
|3
a
-
b
|•|
a
+3
b
|
=
20
3
5
•
15
=
4
3
9
．
点评：本题主要考查两个向量的数量积的定义，求向量的模的方法，属于基础题．
练习册系列答案
相关题目
已知袋中有3个红球2个白球，从中任取一个，恰为红球的概率是（　　）
A、
1
3
B、
1
2
C、
3
5
D、
2
5
已知等差数列{an}中，a3+a8=22，a6=7，则a5的值为（　　）
A、5B、15C、20D、25
某曲线y=f（x）在x=5处的切线方程为y=-x+8，则f（5）+f′（5）=（　　）
A、6B、2C、4D、-2
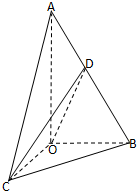如图，在三棱锥A-BOC中，∠OAB=30°，AO⊥平面BOC，AB=4，∠BOC=90°，BO=CO，D是AB的中点．
（1）求证：CO⊥平面AOB；
（2）求异面直线AO与CD所成角的正切值．
已知数列{an}中，a1=1，an+1=
an
an+3
 （n∈N*）．
（1）求证：数列{
1
an
+
1
2
}是等比数列，并求数列{an}的通项an
（2）若数列{bn}满足bn=（3n-1）
n
2n
an，数列{bn}的前n项和为Tn，若不等式（-1）nλ＜Tn对一切n∈N*恒成立，求λ的取值范围．
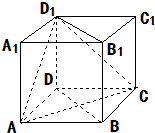如图，在正方体ABCD-A1B1C1D1中．求证：平面ACD1⊥平面BB1D1D．
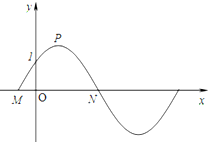已知如图，函数y=2sin（
π
2
x+φ）（0≤φ≤
π
2
，x∈R）的图象与y轴的交点为（0，1）．
（1）求φ的值；
（2）设点P是图象上的最高点，M，N是图象与x轴的交点，求向量
PM
与向量
PN
夹角的余弦值．
设抛物线C：y2=2px（p＞0）的焦点为F，直线l过F且与抛物线C交于M、N两点，已知直线l与x轴垂直时，△OMN的面积为2（O为坐标原点）．
（Ⅰ）求抛物线C的方程；
（Ⅱ）问是否存在直线l，使得以M、N为对角线的正方形的第三个顶点恰好在y轴上，若存在，求直线l的方程；若不存在，说明理由．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网