题目内容
2．设a，b∈R，集合A={1，a+b，a}，B={0，$\frac{b}{a}$，b}，若A=B，则b-a（ ）| A． | 2 | B． | -1 | C． | 1 | D． | -2 |
分析 利用集合相等的性质及集合中元素的性质直接求解．
解答 解：∵a，b∈R，集合A={1，a+b，a}，B={0，$\frac{b}{a}$，b}，A=B，
∴$\left\{\begin{array}{l}{a+b=0}\\{b=1}\end{array}\right.$，
解得a=-1，b=1，
∴b-a=2．
故选：A．
点评 本题考查两实数之差的求法，是基础题，解题时要认真审题，注意集合相等的性质的合理运用．
练习册系列答案
步步高达标卷系列答案
相关题目
12．已知$a={log_3}0.5，b={log_{0.3}}0.2，c={0.5^{0.3}}$，则（ ）
| A． | a＞c＞b | B． | b＞c＞a | C． | b＞a＞c | D． | c＞a＞b |
13．等比数列{an}中，a2+a4=20，a3+a5=40，则a6=（ ）
| A． | 16 | B． | 32 | C． | 64 | D． | 128 |
10．若l，m是两条不同的直线，α是一个平面，则下列命题正确的是（ ）
| A． | 若l∥α，m∥α，则l∥m | B． | 若l⊥m，m?α，则l⊥α | C． | 若l∥α，m?α，则l∥m | D． | 若l⊥α，l∥m，则m⊥α |
7．
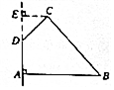如图，在四边形ABCD中，∠DAB=90°，∠ADC=135°，AB=5，CD=2$\sqrt{2}$，AD=2，则四边形ABCD绕AD旋转一周所成几何体的表面积为（ ）
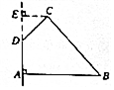如图，在四边形ABCD中，∠DAB=90°，∠ADC=135°，AB=5，CD=2$\sqrt{2}$，AD=2，则四边形ABCD绕AD旋转一周所成几何体的表面积为（ ）| A． | （60+4$\sqrt{2}$）π | B． | （60+8$\sqrt{2}$）π | C． | （56+8$\sqrt{2}$）π | D． | （56+4$\sqrt{2}$）π |
12．定义在R上的偶函数f（x）满足：对于任意的x1，x2∈（-∞，0]（x1≠x2），有（x2-x1）[f（x2）-f（x1）]＞0，则当n∈N*时，有（ ）
| A． | f（-n）＜f（n-1）＜f（n+1） | B． | f（n-1）＜f（-n）＜f（n+1） | C． | f（n+1）＜f（-n）＜f（n-1） | D． | f（n+1）＜f（n-1）＜f（-n） |