题目内容
12.定义在R上的偶函数f(x)满足:对于任意的x1,x2∈(-∞,0](x1≠x2),有(x2-x1)[f(x2)-f(x1)]>0,则当n∈N*时,有( )| A. | f(-n)<f(n-1)<f(n+1) | B. | f(n-1)<f(-n)<f(n+1) | C. | f(n+1)<f(-n)<f(n-1) | D. | f(n+1)<f(n-1)<f(-n) |
分析 根据函数奇偶性和单调性的性质进行转化求解即可.
解答 解:∵对于任意的x1,x2∈(-∞,0](x1≠x2),有(x2-x1)[f(x2)-f(x1)]>0,
∴函数f(x)在(-∞,0]上为增函数,
∵函数f(x)是偶函数,
∴函数f(x)在[0,+∞)上是减函数,
∵当n∈N*时,n+1>n>n-1≥0,
∴f(n+1)<f(n)<f(n-1),
即f(n+1)<f(-n)<f(n-1),
故选:C
点评 本题主要考查函数值的大小比较,根据条件判断函数的单调性是解决本题的关键.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
12.若变量x、y满足$\left\{\begin{array}{l}{x+y≤-1}\\{2x-3y≤9}\\{x≥0}\end{array}\right.$,则x2+y2的最小值是( )
| A. | $\frac{\sqrt{2}}{2}$ | B. | 1 | C. | 3 | D. | $\frac{1}{2}$ |
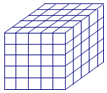 如图,将一个各面都涂了油漆的正方体,切割为125个同样大小的小正方体,经过搅拌后,从中随机取一个小正方体,记它的涂漆面数为X,则X的均值E(X)=$\frac{6}{5}$.
如图,将一个各面都涂了油漆的正方体,切割为125个同样大小的小正方体,经过搅拌后,从中随机取一个小正方体,记它的涂漆面数为X,则X的均值E(X)=$\frac{6}{5}$.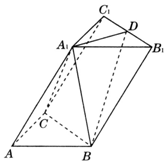 如图,在三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=2,A1A=4,A1在底面ABC的射影为BC的中点,D是B1C1的中点.
如图,在三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=2,A1A=4,A1在底面ABC的射影为BC的中点,D是B1C1的中点.