题目内容
14.已知圆C:x2+y2-4x-14y+45=0及点Q(-2,3).(1)若M为圆C上任一点,求|MQ|的最大值和最小值;
(2)若实数m,n满足m2+n2-4m-14n+45=0,求k=$\frac{n-3}{m+2}$的最大值和最小值.
分析 (1)求出|QC|,即可求|MQ|的最大值和最小值;
(2)由题意,(m,n)是圆C上一点,k表示圆上任意一点与(-2,3)连线的斜率,设直线方程为y-3=k(x+2),直线与圆C相切时,k取得最值.
解答 解:(1)圆C:x2+y2-4x-14y+45=0可化为(x-2)2+(y-7)2=8,圆心坐标为C(2,7),半径r=2$\sqrt{2}$,
|QC|=$\sqrt{(2+2)^{2}+(7-3)^{2}}$=4$\sqrt{2}$,|MQ|max=4$\sqrt{2}$+2$\sqrt{2}$=6$\sqrt{2}$,|MQ|min=4$\sqrt{2}-2\sqrt{2}$=2$\sqrt{2}$;
(2)由题意,(m,n)是圆C上一点,k表示圆上任意一点与(-2,3)连线的斜率,
设直线方程为y-3=k(x+2),直线与圆C相切时,k取得最值,即$\frac{|2k-7+2k+3|}{\sqrt{{k}^{2}+1}}$=2$\sqrt{2}$,
∴k=2$±\sqrt{3}$,
∴k的最大值为2+$\sqrt{3}$,最小值为2-$\sqrt{3}$.
点评 本题考查直线与圆的位置关系,考查点到直线的距离公式,属于中档题.

练习册系列答案
相关题目
9.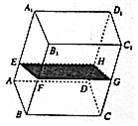 如图,在透明塑料制成的长方体ABCD-A1B1C1D1容器内灌进一些水,将容器底面一边BC固定于地面上,再将容器倾斜,随着倾斜度的不同,有下列四个说法:
如图,在透明塑料制成的长方体ABCD-A1B1C1D1容器内灌进一些水,将容器底面一边BC固定于地面上,再将容器倾斜,随着倾斜度的不同,有下列四个说法:
①水的部分始终呈棱柱状;
②水面四边形EFGH的面积不改变;
③棱A1D1始终与水面EFGH平行;
④当E∈AA1时,AE+BF是定值.其中正确说法的是( )
 如图,在透明塑料制成的长方体ABCD-A1B1C1D1容器内灌进一些水,将容器底面一边BC固定于地面上,再将容器倾斜,随着倾斜度的不同,有下列四个说法:
如图,在透明塑料制成的长方体ABCD-A1B1C1D1容器内灌进一些水,将容器底面一边BC固定于地面上,再将容器倾斜,随着倾斜度的不同,有下列四个说法:①水的部分始终呈棱柱状;
②水面四边形EFGH的面积不改变;
③棱A1D1始终与水面EFGH平行;
④当E∈AA1时,AE+BF是定值.其中正确说法的是( )
| A. | ②③④ | B. | ①②④ | C. | ①③④ | D. | ①②③ |
6.“2<m<6”是“方程$\frac{{x}^{2}}{m-2}$+$\frac{{y}^{2}}{6-m}$=1表示椭圆”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不必要也不充分条件 |
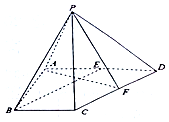 如图,在四棱锥P-ABCD中,△PCD为等边三角形,底面ABCD为直角梯形,AB⊥AD,AD∥BC,AD=2BC=2,AB=$\sqrt{3}$,点E、F分别为AD、CD的中点.
如图,在四棱锥P-ABCD中,△PCD为等边三角形,底面ABCD为直角梯形,AB⊥AD,AD∥BC,AD=2BC=2,AB=$\sqrt{3}$,点E、F分别为AD、CD的中点.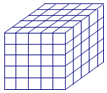 如图,将一个各面都涂了油漆的正方体,切割为125个同样大小的小正方体,经过搅拌后,从中随机取一个小正方体,记它的涂漆面数为X,则X的均值E(X)=$\frac{6}{5}$.
如图,将一个各面都涂了油漆的正方体,切割为125个同样大小的小正方体,经过搅拌后,从中随机取一个小正方体,记它的涂漆面数为X,则X的均值E(X)=$\frac{6}{5}$.