Question

7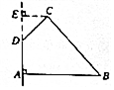．如图，在四边形ABCD中，∠DAB=90°，∠ADC=135°，AB=5，CD=2$\sqrt{2}$，AD=2，则四边形ABCD绕AD旋转一周所成几何体的表面积为（　　）

• A． （60+4$\sqrt{2}$）π
• B． （60+8$\sqrt{2}$）π
• C． （56+8$\sqrt{2}$）π
• D． （56+4$\sqrt{2}$）π

Answer 1

分析 旋转后的几何体是圆台除去一个倒放的圆锥，根据题目所给数据，求出圆台的侧面积、圆锥的侧面积、圆台的底面积，即可求出几何体的表面积．

解答 解：四边形ABCD绕AD旋转一周所成的几何体，如右图：
S_表面=S_{圆台下底面}+S_圆台侧面+S_圆锥侧面=
πr₂²+π（r₁+r₂）l₂+πr₁l₁=$π×{5}^{2}+π×（2+5）×5+π×2×2\sqrt{2}$=（60+4$\sqrt{2}$）π，
故选：A．

点评 本题是基础题，考查旋转体的表面积，转化思想的应用，计算能力的考查，都是为本题设置的障碍，仔细分析旋转体的结构特征，为顺利解题创造依据．