等比数列{an}中.a2+a4=20.a3+a5=40.则a6=( )A．16B．32C．64D．128 题目和参考答案——青夏教育精英家教网—

题目内容

13．等比数列{a_n}中，a₂+a₄=20，a₃+a₅=40，则a₆=（　　）

A．

B．

C．

D．

128

分析由等比数列通项公式列出方程组，求出首项和公差，由此能求出a₆．

解答解：∵等比数列{a_n}中，a₂+a₄=20，a₃+a₅=40，
∴$\left\{\begin{array}{l}{{a}_{1}q+{a}_{1}{q}^{3}=20}\\{{a}_{1}{q}^{2}+{a}_{1}{q}^{4}=40}\end{array}\right.$，解得a=2，q=2，
∴a₆=2×2⁵=64．
故选：C．

点评本题考查等比数列的第6项的求法，是基础题，解题时要认真审题，注意等比数列的性质的合理运用．

练习册系列答案

特级教师小学毕业升学系统总复习系列答案

提分计划单元期末系列答案

经纶学典提优作业本系列答案

题粹系列答案

相关题目

3．

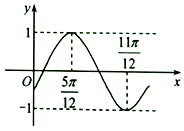函数f（x）=sin（ωx+φ）（ω＞0，-$\frac{π}{2}$＜φ＜$\frac{π}{2}$）的部分图象如图所示，则f（0）=$-\frac{{\sqrt{3}}}{2}$．

4．

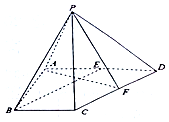如图，在四棱锥P-ABCD中，△PCD为等边三角形，底面ABCD为直角梯形，AB⊥AD，AD∥BC，AD=2BC=2，AB=$\sqrt{3}$，点E、F分别为AD、CD的中点．
（1）求证：直线BE∥平面PCD；
（2）求证：平面PAF⊥平面PCD；
（3）若PB=$\sqrt{3}$，求直线PB与平面PAF所成的角．

1．已知$tanθ=\frac{1}{2}$，则$tan（{\frac{π}{4}-2θ}）$=（　　）

8．已知{a_n}是等比数列，a₅=$\frac{1}{2}，4{a_3}+{a_7}$=2，则a₇=1．

18．在△ABC中，若BC=2，A=120°，则$\overrightarrow{AB}$•$\overrightarrow{CA}$的最大值为（　　）

5．S_n为数列{a_n}的前n项和，已知a_n＞0，a_n²+a_n=2S_n．
（1）求数列{a_n}的通项公式；
（2）若b_n=$\frac{{a}_{n}}{{2}^{{a}_{n-1}}}$，求数列{b_n}的前n项和T_n．

2．设a，b∈R，集合A={1，a+b，a}，B={0，$\frac{b}{a}$，b}，若A=B，则b-a（　　）

3．

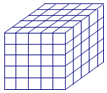如图，将一个各面都涂了油漆的正方体，切割为125个同样大小的小正方体，经过搅拌后，从中随机取一个小正方体，记它的涂漆面数为X，则X的均值E（X）=$\frac{6}{5}$．

试题分类