Question

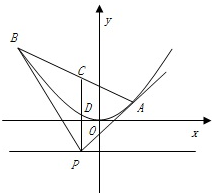设P是直线y=-2上一点，过点P作抛物线x²=4y的两条切线PA，PB和平行于y轴的直线l，切点分别为A，B，直线l与AB和抛物线分别相交于C，D，记PA，PB的斜率分别为k₁，k₂．
（1）若k₁+k₂=2，求点P的坐标；
（2）求证：|AC|=|BC|，且|CD|=|PD|．

Answer 1

考点：直线与圆锥曲线的综合问题

专题：圆锥曲线中的最值与范围问题

分析：（1）设A（x₁，y₁），B（x₂，y₂），由y′=

1

2

x，得切线PA：y=

1

2

x1x-y1，切线PB：y=

1

2

x2x-y2，设P（t，-2），得直线AB的方程为

1

2

tx-y+2=0，联立

x2=4y 1 2 tx-y+2=0

，得x²-2tx+8=0，由此利用韦达定理能求出点P（2，-2）．
（2）联立

x2=4y 1 2 tx-y+2=0

，得x²-2tx-8=0，x₁+x₂=2t，x₁x₂=-8，由此利用韦达定理得线段AB的中点坐标为（t，

1

2

 2t +2），把把x=t代入直线AB的方程

1

2

tx-y+2=0，得C（t，

1

2

t2+2），从而得到|AC|=|BC|，把x=t代入抛物线x²=4y，得D（t，

t2

4

），从而得到|CD|=|PD|．

解答： 解：（1）设A（x₁，y₁），B（x₂，y₂），
∵y′=

1

2

x，∴切线PA：y-y₁=

1

2

x1（x-x₁），即y=

1

2

x1x-y1，
切线PB：y-y2=

1

2

x2(x-x2)，即y=

1

2

x2x-y2，
∵PA，PB的斜率分别为k₁，k₂，k₁+k₂=2，
∴

1

2

(x1+x2)=2，即x₁+x₂=4，
∵P是直线y=-2上一点，∴设P（t，-2），
则由P（t，-2）是PA和PB的交点，得

1 2 x1t-y1=-2 1 2 x2t-y2=-2

，
∴直线AB的方程为

1

2

tx-y+2=0，过定点（0，2）
联立

x2=4y 1 2 tx-y+2=0

，得x²-2tx+8=0，
△=4t²-32＞0，解得t＞2

2

或t＜-2

2

，
x₁+x₂=2t，又x₁+x₂=4，∴2t=4，解得t=2，
∴点P（2，-2）．
（2）∵联立

x2=4y 1 2 tx-y+2=0

，得x²-2tx-8=0，
∴x₁+x₂=2t，x₁x₂=-8，
y₁+y₂=

x12

4

+

x22

4

=

1

4

[（x₁+x₂）²-2x₁x₂]=t²+4，
∴线段AB的中点坐标为（t，

1

2

 2t +2），
∵过点P（t，-2）作平行于y轴的直线l，直线l与AB和抛物线分别相交于C，D，
把x=t代入直线AB的方程

1

2

tx-y+2=0，得y=

1

2

t2+2，
∴C（t，

1

2

t2+2），
∴C是线段AB的中点，∴|AC|=|BC|，
把x=t代入抛物线x²=4y，得y=

t2

4

，∴D（t，

t2

4

），
∴D是线段PC的中点，∴|CD|=|PD|．

点评：本题考查点的坐标的求法，考查线段相等的证明，解题时要认真审题，注意导数的几何意义、切线方程，抛物线性质等知识点的合理运用．