题目内容
已知圆锥曲线C:
(α为参数)和定点A(0,
),F1、F2是此圆锥曲线的左、右焦点,以原点O为极点,以x轴的正半轴为极轴建立极坐标系.
(1)求直线AF2的直角坐标方程;
(2)经过点F1且与直线AF2垂直的直线l交此圆锥曲线于M、N两点,求|MF1|-|NF1|的值.
|
| 3 |
(1)求直线AF2的直角坐标方程;
(2)经过点F1且与直线AF2垂直的直线l交此圆锥曲线于M、N两点,求|MF1|-|NF1|的值.
考点:椭圆的参数方程,直线与圆锥曲线的关系
专题:计算题,直线与圆,圆锥曲线的定义、性质与方程,坐标系和参数方程
分析:(1)求出椭圆方程的普通方程,求出焦点,运用直线方程的截距式写出直线AF2的直角坐标方程;
(2)运用两直线垂直的条件,求得直线l的斜率和倾斜角,写出参数方程,代入椭圆方程,由韦达定理及参数的几何意义,即可得到所求.
(2)运用两直线垂直的条件,求得直线l的斜率和倾斜角,写出参数方程,代入椭圆方程,由韦达定理及参数的几何意义,即可得到所求.
解答:
解:(1)曲线C:
可化为
+
=1,
其轨迹为椭圆,焦点为F1(-1,0),F2(1,0).
经过A(0,
)和F2(1,0)的直线方程为
+
=1,
即
x+y-
=0;
(2)由(1)知,直线AF2的斜率为-
,
因为l⊥AF2,所以l的斜率为
,倾斜角为30°,
所以l的参数方程为
(t为参数),
代入椭圆C的方程中,得13t2-12
t-36=0.
因为M,N在点F1的两侧,
所以|MF1|-|NF1|=|t1+t2|=
.
|
| x2 |
| 4 |
| y2 |
| 3 |
其轨迹为椭圆,焦点为F1(-1,0),F2(1,0).
经过A(0,
| 3 |
| x |
| 1 |
| y | ||
|
即
| 3 |
| 3 |
(2)由(1)知,直线AF2的斜率为-
| 3 |
因为l⊥AF2,所以l的斜率为
| ||
| 3 |
所以l的参数方程为
|
代入椭圆C的方程中,得13t2-12
| 3 |
因为M,N在点F1的两侧,
所以|MF1|-|NF1|=|t1+t2|=
12
| ||
| 13 |
点评:本题考查椭圆的参数方程和普通方程的互化,考查椭圆的性质和直线方程的参数式和运用,考查运算能力,属于基础题.

练习册系列答案
相关题目
已知{an}、{bn}是两个等差数列,其中a1=3,b1=-3,且a19-b19=16,那么a10-b10的值为( )
| A、-6 | B、6 | C、0 | D、11 |
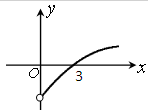 已知f(x)是定义在(-∞,0)∪(0,+∞)上的偶函数,当x>0时,y=f(x)的图象如图所示,解不等式xf(x)<0.
已知f(x)是定义在(-∞,0)∪(0,+∞)上的偶函数,当x>0时,y=f(x)的图象如图所示,解不等式xf(x)<0.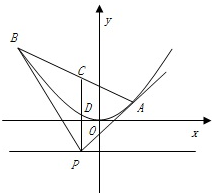 设P是直线y=-2上一点,过点P作抛物线x2=4y的两条切线PA,PB和平行于y轴的直线l,切点分别为A,B,直线l与AB和抛物线分别相交于C,D,记PA,PB的斜率分别为k1,k2.
设P是直线y=-2上一点,过点P作抛物线x2=4y的两条切线PA,PB和平行于y轴的直线l,切点分别为A,B,直线l与AB和抛物线分别相交于C,D,记PA,PB的斜率分别为k1,k2.