题目内容
抛物线M:y2=2px(p>0)的准线过椭圆N:
+y2=1的左焦点,以原点为圆心,以t(t>0)为半径的圆分别与抛物线M在第一象限的图象以及y轴的正半轴相交于点A和B,直线AB与x轴相交于点C.
(Ⅰ)求抛物线M的方程;
(Ⅱ)设点A的横坐标为a,点C的横坐标为c,抛物线M上点D的横坐标为a+2,求直线CD的斜率.
| 4x2 |
| 5 |
(Ⅰ)求抛物线M的方程;
(Ⅱ)设点A的横坐标为a,点C的横坐标为c,抛物线M上点D的横坐标为a+2,求直线CD的斜率.
考点:抛物线的简单性质
专题:圆锥曲线的定义、性质与方程
分析:(Ⅰ)由椭圆方程求出椭圆左焦点坐标,得到抛物线准线方程,从而求得p值,则抛物线方程可求;
(Ⅱ)写出A的坐标,由|OA|=t列式求得t与A的坐标间的关系,求出直线BC的方程,把A代入BC方程,得到a,c的关系,然后直接代入斜率公式求直线CD的斜率.
(Ⅱ)写出A的坐标,由|OA|=t列式求得t与A的坐标间的关系,求出直线BC的方程,把A代入BC方程,得到a,c的关系,然后直接代入斜率公式求直线CD的斜率.
解答:
解:(Ⅰ)∵椭圆N:
+y2=1,
∴c2=a2-b2=
-1=
,
∴椭圆的左焦点为F1(-
,0),
∴-
=-
,则p=1.
故M:y2=2x;
(Ⅱ)由题意知,A(a,2a),
∵|OA|=t,
∴a2+2a=t2.
由于t>0,故有t=
①
由点B(0,t),C(c,0)的坐标知,
直线BC的方程为
+
=1.
又∵A在直线BC上,故有
+
=1.
将①代入上式,得:
+
=1,解得c=a+2+
.
又∵D(a+2,2
),
∴直线CD的斜率为:
kCD=
=
=
=-1.
| 4x2 |
| 5 |
∴c2=a2-b2=
| 5 |
| 4 |
| 1 |
| 4 |
∴椭圆的左焦点为F1(-
| 1 |
| 2 |
∴-
| p |
| 2 |
| 1 |
| 2 |
故M:y2=2x;
(Ⅱ)由题意知,A(a,2a),
∵|OA|=t,
∴a2+2a=t2.
由于t>0,故有t=
| a2+2a |
由点B(0,t),C(c,0)的坐标知,
直线BC的方程为
| x |
| c |
| y |
| t |
又∵A在直线BC上,故有
| a |
| c |
| ||
| t |
将①代入上式,得:
| a |
| c |
| ||
|
| 2(a+2) |
又∵D(a+2,2
| 2(a+2) |
∴直线CD的斜率为:
kCD=
| ||
| a+2-c |
| ||
a+2-(a+2+
|
| ||
-
|
点评:本题主要抛物线方程的求法,考查了直线与圆锥曲线位置关系的应用,解答此题的关键是对抛物线定义的灵活应用,是高考试卷中的压轴题.

练习册系列答案
相关题目
设l是空间中的一条直线,α,β是两个不同的平面,已知l⊥α,则“l⊥β”是“α∥β”的( )
| A、充要条件 |
| B、充分不必要条件 |
| C、必要不充分条件 |
| D、既不充分也不必要条件 |

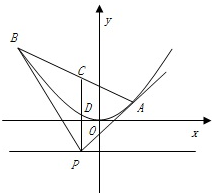 设P是直线y=-2上一点,过点P作抛物线x2=4y的两条切线PA,PB和平行于y轴的直线l,切点分别为A,B,直线l与AB和抛物线分别相交于C,D,记PA,PB的斜率分别为k1,k2.
设P是直线y=-2上一点,过点P作抛物线x2=4y的两条切线PA,PB和平行于y轴的直线l,切点分别为A,B,直线l与AB和抛物线分别相交于C,D,记PA,PB的斜率分别为k1,k2.