题目内容
7.设矩阵M=$|\begin{array}{l}{m}&{2}\\{2}&{-3}\end{array}|$的一个特征值λ对应的特征向量为$[\begin{array}{l}{1}\\{-2}\end{array}]$,求m与λ的值.分析 推导出$\left\{{\begin{array}{l}{m-4=λ}\\{2+6=-2λ}\end{array}}\right.$,由此能求出结果.
解答 解:∵矩阵M=$|\begin{array}{l}{m}&{2}\\{2}&{-3}\end{array}|$的一个特征值λ对应的特征向量为$[\begin{array}{l}{1}\\{-2}\end{array}]$,
∴$\left\{{\begin{array}{l}{m-4=λ}\\{2+6=-2λ}\end{array}}\right.$,…(8分)
解得m=0,λ=-4.…(10分)
点评 本题考查实数值的求法,是基础题,解题时要认真审题,注意特征向量的性质的合理运用.

练习册系列答案
相关题目
15.已知函数$f(x)=1+x-\frac{x^2}{2}+\frac{x^3}{3}-…+\frac{{{x^{2017}}}}{2017}$,设F(x)=f(x+4),且F(x)的零点均在区间(a,b)内,其中a,b∈Z,a<b,则F(x)>0的最小整数解为( )
| A. | -1 | B. | 0 | C. | -5 | D. | -4 |
2.一直线l与平行四边形ABCD中的两边AB、AD分别交于E、F,且交其对角线AC于K,若$\overrightarrow{AB}$=2$\overrightarrow{AE}$,$\overrightarrow{AD}$=3$\overrightarrow{AF}$,$\overrightarrow{AC}$=λ$\overrightarrow{AK}$(λ∈R),则λ=( )
| A. | 2 | B. | $\frac{5}{2}$ | C. | 3 | D. | 5 |
12.要得到函数$y=sin({3x-\frac{π}{6}})$的图象,只需将函数y=cos3x的图象( )
| A. | 向右平移$\frac{2π}{9}$个单位 | B. | 向左平移$\frac{2π}{9}$个单位 | ||
| C. | 向右平移$\frac{2π}{3}$个单位 | D. | 向左平移$\frac{2π}{3}$个单位 |
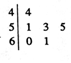 为了检查某高三毕业班学生的体重情况,从该班随机抽取了6位学生进行称重,如图为6位学生体重的茎叶图(单位:kg),其中图中左边是体重的十位数字,右边是个位数字,则这6位学生体重的平均数为( )
为了检查某高三毕业班学生的体重情况,从该班随机抽取了6位学生进行称重,如图为6位学生体重的茎叶图(单位:kg),其中图中左边是体重的十位数字,右边是个位数字,则这6位学生体重的平均数为( )