题目内容
已知数列{an}的每一项都为正数,a1=
,a2=
,且对满足s+t=p+q的正整数s,t,p,q,都有
=
.记bn=
.
(1)证明:数列{bn}是等比数列;
(2)求数列{an}的通项公式.
| 1 |
| 2 |
| 4 |
| 5 |
| as+at |
| (1+as)(1+at) |
| ap+aq |
| (1+ap)(1+aq) |
| 1-an |
| 1+an |
(1)证明:数列{bn}是等比数列;
(2)求数列{an}的通项公式.
考点:数列递推式,等比数列的性质
专题:等差数列与等比数列
分析:(1)法1:根据递推关系求出
是常数,即可证明数列{bn}是等比数列;
法2:利用等比数列的性质去证明等比数列.
(2)根据数列{bn}是等比数列,先求出{bn}的通项公式,然后即可求数列{an}的通项公式.
| bn+1 |
| bn |
法2:利用等比数列的性质去证明等比数列.
(2)根据数列{bn}是等比数列,先求出{bn}的通项公式,然后即可求数列{an}的通项公式.
解答:
解:(1)证法一:
由已知
=
,代入a1=
,a2=
可得
=
⇒5-
=6-
⇒
=
+1⇒an+1=
由定义对任意的n∈N*,
=
•
=
•
=
•
=
从而数列{bn}是以
为公比的等比数列.
证法二:
由bn=
⇒an=
代入已知可得
=
,
整理得到(
+
)(1+bs)(1+bt)=(
+
)(1+bp)(1+bq)⇒bs•bt=bp•bq,
即对满足s+t=p+q的正整数s,t,p,q,均有bs•bt=bp•bq,符合等比数列性质,又通过取特殊值可得
=
=
.从而数列{bn}是以
为公比的等比数列.
(2)经计算b1=
=
=
,
从而bn=(
)n⇒an=
=
,n∈N*
由已知
| a2+an |
| (1+a2)(1+an) |
| a1+an+1 |
| (1+a1)(1+an+1) |
| 1 |
| 2 |
| 4 |
| 5 |
| 4+5an |
| 9(1+an) |
| 1+2an+1 |
| 3(1+an+1) |
| 1 |
| 1+an |
| 3 |
| 1+an+1 |
| 3 |
| 1+an+1 |
| 1 |
| 1+an |
| 2an+1 |
| an+2 |
由定义对任意的n∈N*,
| bn+1 |
| bn |
| 1-an+1 |
| 1+an+1 |
| 1+an |
| 1-an |
1-
| ||
1+
|
| 1+an |
| 1-an |
| 1-an |
| 3(1+an) |
| 1+an |
| 1-an |
| 1 |
| 3 |
从而数列{bn}是以
| 1 |
| 3 |
证法二:
由bn=
| 1-an |
| 1+an |
| 1-bn |
| 1+bn |
| ||||
(1+
|
| ||||
(1+
|
整理得到(
| 1-bs |
| 1+bs |
| 1-bt |
| 1+bt |
| 1-bp |
| 1+bp |
| 1-bq |
| 1+bq |
即对满足s+t=p+q的正整数s,t,p,q,均有bs•bt=bp•bq,符合等比数列性质,又通过取特殊值可得
| bn+1 |
| bn |
| b2 |
| b1 |
| 1 |
| 3 |
| 1 |
| 3 |
(2)经计算b1=
| 1-a1 |
| 1+a1 |
1-
| ||
1+
|
| 1 |
| 3 |
从而bn=(
| 1 |
| 3 |
| 1-bn |
| 1+bn |
| 3n-1 |
| 3n+1 |
点评:本题主要考查等比数列的证明以及数列通项公式的计算,利用数列的递推关系是解决本题的关键.

练习册系列答案
 学习实践园地系列答案
学习实践园地系列答案
相关题目
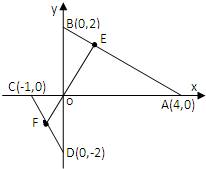 在直角坐标系中,已知A(4,0),B(0,2),C(0,-2),点E在线段AB(不含端点)上,点F在线段CD上,E、O、F三点共线.
在直角坐标系中,已知A(4,0),B(0,2),C(0,-2),点E在线段AB(不含端点)上,点F在线段CD上,E、O、F三点共线.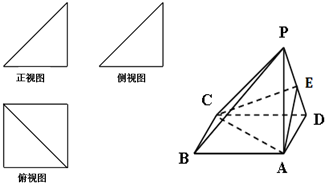 一个简单多面体的直观图和三视图如图所示,它的正视图和侧视图都是腰长为1的等腰直角三角形,俯视图为正方形.
一个简单多面体的直观图和三视图如图所示,它的正视图和侧视图都是腰长为1的等腰直角三角形,俯视图为正方形.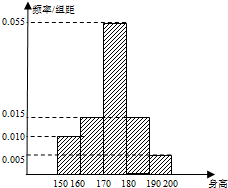 某学校高三年级有学生1000名,经调查研究,其中750名同学经常参加体育锻炼(称为A类同学),另外250名同学不经常参加体育锻炼(称为B类同学),现用分层抽样方法(按A类、B类分二层)从该年级的学生中共抽查100名同学.
某学校高三年级有学生1000名,经调查研究,其中750名同学经常参加体育锻炼(称为A类同学),另外250名同学不经常参加体育锻炼(称为B类同学),现用分层抽样方法(按A类、B类分二层)从该年级的学生中共抽查100名同学.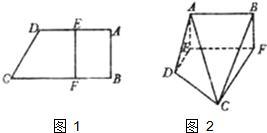 如图1,在直角梯形ABCD中,AD∥BC,∠ABC=90°,当E、F分别在线段AD、BC上,且EF⊥BC,AD=4,CB=6,AE=2.现将梯形ABCD沿EF折叠,如图2,使平面ABFE与平面EFCD垂直.
如图1,在直角梯形ABCD中,AD∥BC,∠ABC=90°,当E、F分别在线段AD、BC上,且EF⊥BC,AD=4,CB=6,AE=2.现将梯形ABCD沿EF折叠,如图2,使平面ABFE与平面EFCD垂直.