题目内容
18．已知m＞2，若函数g（x）=$\left\{\begin{array}{l}{{m}^{x}-2，0＜x≤2}\\{g（x-2）+m-2，2＜x≤4}\end{array}\right.$，则方程g（g（x））-m+3=0的根的个数最多有（ ）| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
分析 做出g（x）的函数图象，判断两段函数图象的关系，令g（x）=t，判断关于t的方程g（t）-m+3=0的根的个数及根所在的区间，总而得出关于x的方程g（x）=t的根的个数．
解答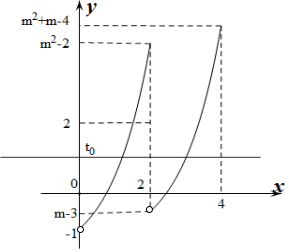 
解：由题意可知g（x）在（2，4]上的图象是由（0，2]上的图象向右平移2个单位再向上平移m-2个单位得到的．
做出g（x）的大致函数图象如图所示：
∵m＞2，∴m2-2-（m-3）=m2-m+1＞0，
∴m2-2＞m-3，
设g（x）=t，由g（g（x））-m+3=0得g（t）=m-3，
∴关于t的方程g（t）=m-3有且只有一解t0，且t0∈（0，2），
∵m＞2，∴m2-2＞2，
∴当m-3≥2时，g（x）=t0只有1解，
当m-3≤0时，g（x）=t0有2解，
当0＜m-3＜2时，g（x）=t0可能有1解，也可能有2解．
∴方程g（g（x））-m+3=0的根的个数最多有2个．
故选B．
点评 本题考查了函数图象的变换，方程根的个数与函数图象的关系，属于中档题．
练习册系列答案
相关题目
6．一个几何体的三视图如图所示，则这个几何体的表面积为（ ）
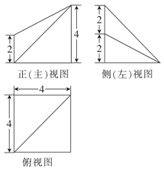
| A． | 40+8$\sqrt{2}$+4$\sqrt{6}$ | B． | 40+8$\sqrt{3}$+4$\sqrt{6}$ | C． | 48+8$\sqrt{3}$ | D． | 48+8$\sqrt{2}$ |
3．若集合A={x|-4＜x＜3}，B={x|x＜cos5π}，则A∩B等于（ ）
| A． | （-4，0） | B． | （-4，-1） | C． | （-4，1） | D． | （-3，-1） |
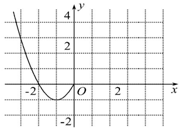已知函数f（x）是定义在R上的偶函数，现已画出函数f（x）在y轴左侧的图象（二次函数图象的一部分），如图所示，请根据图象：