题目内容
6.一个几何体的三视图如图所示,则这个几何体的表面积为( )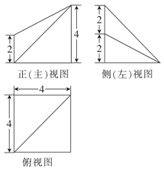
| A. | 40+8$\sqrt{2}$+4$\sqrt{6}$ | B. | 40+8$\sqrt{3}$+4$\sqrt{6}$ | C. | 48+8$\sqrt{3}$ | D. | 48+8$\sqrt{2}$ |
分析 由已知中的三视图,画出几何体的直观图,进而求出各个面的面积,可得答案.
解答 解:由已知中的三视图,可得几何体的直观图如图所示,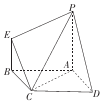
底面ABCD的面积为:4×4=16,
面EBC的面积为:$\frac{1}{2}$×2×4=4,
面APD的面积为:$\frac{1}{2}$×4×4=8,
面ABEP的面积为:$\frac{1}{2}$×(2+4)×4=12,
面PCD的面积为:$\frac{1}{2}$×4×4$\sqrt{2}$=8$\sqrt{2}$,
面PCE的面积为:$\frac{1}{2}$×4$\sqrt{3}$×2$\sqrt{2}$=4$\sqrt{6}$,
故几何体的表面积S=40+8$\sqrt{2}$+4$\sqrt{6}$
故选:A
点评 本题考查的知识点多面体的体积和表面积,简单几何体的三视图,难度中档.

练习册系列答案
相关题目
14.已知二次函数y=f(x)的开口向下,且满足f(2+x)=f(2-x),则( )
| A. | f(0)<f(3)<f(5) | B. | f(0)<f(5)<f(3) | C. | f(5)<f(3)<f(0) | D. | f(5)<f(0)<f(3) |
18.已知m>2,若函数g(x)=$\left\{\begin{array}{l}{{m}^{x}-2,0<x≤2}\\{g(x-2)+m-2,2<x≤4}\end{array}\right.$,则方程g(g(x))-m+3=0的根的个数最多有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
15.某几何体的三视图如图,其正视图中的曲线部分为半圆,则该几何体的表面积为( )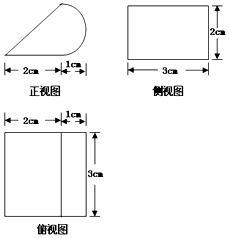

| A. | (19+π)cm2 | B. | (22+4π)cm2 | C. | (10+6$\sqrt{2}$+4π)cm2 | D. | (13+6$\sqrt{2}$+4π)cm2 |