题目内容
7．光线经过点A（1，2）射到y轴上，反射后经过点B（4，-3），则反射光线所在直线的方程为x+y-1=0．分析 由反射定律可得点A（1，2）关于y轴的对称点A′（1，2）在反射光线所在的直线上，再根据点B（4，-3）也在反射光线所在的直线上，用两点式求得反射光线所在的直线方程．
解答 解：点A（1，2）关于y轴的对称点的坐标为A′（-1，2），在反射光线所在的直线上，
再根据点B（4，-3）也在反射光线所在的直线上，
用两点式求得反射光线所在的直线方程为$\frac{y-2}{-3-2}=\frac{x+1}{4+1}$，即x+y-1=0．
故答案为：x+y-1=0．
点评 本题主要考查求一个点关于直线的对称点的坐标，用两点式求直线的方程，属于基础题．
练习册系列答案
相关题目
18．已知m＞2，若函数g（x）=$\left\{\begin{array}{l}{{m}^{x}-2，0＜x≤2}\\{g（x-2）+m-2，2＜x≤4}\end{array}\right.$，则方程g（g（x））-m+3=0的根的个数最多有（ ）
| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
15．某几何体的三视图如图，其正视图中的曲线部分为半圆，则该几何体的表面积为（ ）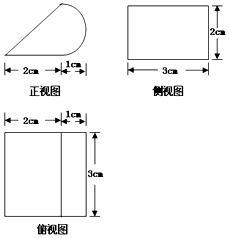
| A． | （19+π）cm2 | B． | （22+4π）cm2 | C． | （10+6$\sqrt{2}$+4π）cm2 | D． | （13+6$\sqrt{2}$+4π）cm2 |
2．2016年8月江西某高校的成立了一个社会实践调查小组，在对大学生的“4G使用流量问题”的调查中，随机发放了120份问卷，对收回的100份有效问卷进行统计，得到如下2×2列联表：
（1）现已按4G使用流量问题采用分层抽样从45份男生问卷中抽取了9份问卷，试问应该从“流量超过1000M”和“流量没有超过1000M”各抽取多少人？
（2）如果认为良好“4G使用流量问题”与性别有关犯错误的概率不超过P，那么根据临界值表最精确的P的值应为多少？请说明理由．
附：独立性检验统计量K2=$\frac{{n{{（ad-bc）}^2}}}{（a+b）（c+d）（a+c）（b+d）}$，其中n=a+b+c+d，
独立性检验临界表：
| 流量超过1000M | 流量没有超过1000M | 合计 | |
| 男 | 20 | 25 | 45 |
| 女 | 40 | 15 | 55 |
| 合计 | 60 | 40 | 100 |
（2）如果认为良好“4G使用流量问题”与性别有关犯错误的概率不超过P，那么根据临界值表最精确的P的值应为多少？请说明理由．
附：独立性检验统计量K2=$\frac{{n{{（ad-bc）}^2}}}{（a+b）（c+d）（a+c）（b+d）}$，其中n=a+b+c+d，
独立性检验临界表：
| P（K2≥k0） | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| k0 | 1.323 | 2.072 | 2.706 | 3.840 | 5.024 |
12．已知双曲线E：$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的左焦点为F（-2，0），过点F的直线交双曲线于AB两点．若AB的中点坐标为（-3，-1），则E的方程为（ ）
| A． | $\frac{{x}^{2}}{9}$-$\frac{{y}^{2}}{1}$=1 | B． | $\frac{{x}^{2}}{1}$-$\frac{{y}^{2}}{3}$=1 | C． | $\frac{{x}^{2}}{3}$-$\frac{{y}^{2}}{1}$=1 | D． | $\frac{{x}^{2}}{1}$-$\frac{{y}^{2}}{9}$=1 |
17．在△ABC中，“cosB=$\frac{1}{2}$”是“A、B、C成等差数列”的（ ）
| A． | 充分非必要条件 | B． | 必要非充分条件 | ||
| C． | 充要条件 | D． | 既非充分又非必要条件 |