题目内容
9．如图，矩形ABCD中，$AB=\sqrt{2}AD$，E为边AB的中点，将△ADE沿直线DE翻转成△A1DE．若M为线段A1C的中点，则在△ADE翻转过程中，下列结论中：①|BM|是定值；②点M在球面上运动；③DE⊥A1C；④MB∥平面A1DE．其中错误的有（ ）个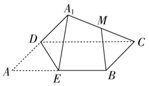
| A． | 0 | B． | 1 | C． | 2 | D． | 3 |
分析 取DC中点N，连MN，NB，则MN∥A1D，NB∥DE，从而MB∥面A1DE；由MN=$\frac{1}{2}$A1D，NB=DE，根据余弦定理得到MB是定值；M是在以B为圆心，MB为半径的球上；A1C在平面ABCD中的射影为AC，AC与DE不垂直．
解答 解：取DC中点N，连MN，NB，MN∥A1D，NB∥DE，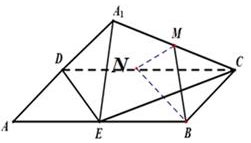
∴面MNB∥面A1DE，MB?面MNB，
∴MB∥面A1DE，故④正确；
∠A1DE=∠MNB，MN=$\frac{1}{2}$A1D为定值，NB=DE为定值，
根据余弦定理得到：MB2=MN2+NB2-2MN•NB•cos∠MNB，
所以MB是定值．故①正确．
B是定点，所以M是在以B为圆心，MB为半径的球上，故②正确．
A1C在平面ABCD中的射影为AC，AC与DE不垂直，故③不正确．
故选：B．
点评 本题考查命题命题真假的判断，是基础题，解题时要认真审题，注意空间中线线、线面、面面间的位置关系的合理运用．
练习册系列答案
寒假天地重庆出版社系列答案
相关题目
4．
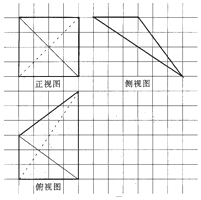如图，网格纸上小正方形的边长为1，下图画出的是某空间几何体的三视图，则该几何体的最短棱长为（ ）
如图，网格纸上小正方形的边长为1，下图画出的是某空间几何体的三视图，则该几何体的最短棱长为（ ）| A． | 4 | B． | 5 | C． | 4$\sqrt{2}$ | D． | $\sqrt{41}$ |
14．已知二次函数y=f（x）的开口向下，且满足f（2+x）=f（2-x），则（ ）
| A． | f（0）＜f（3）＜f（5） | B． | f（0）＜f（5）＜f（3） | C． | f（5）＜f（3）＜f（0） | D． | f（5）＜f（0）＜f（3） |