题目内容
求sinx=
在区间[-π,π]内解的个数.
| 1 |
| x |
考点:正弦函数的图象
专题:作图题,三角函数的图像与性质
分析:函数y=sinx与y=
的图象交点个数等于方程解的个数.在同一坐标系内作出两个函数y=sinx,y=
在[-π,π]内的图象,不难看出它们有2个交点.
| 1 |
| x |
| 1 |
| x |
解答:
 解:函数y=sinx与y=
解:函数y=sinx与y=
的图象交点个数等于方程解的个数.
在同一坐标系内作出两个函数y=sinx,y=
在[-π,π]内的图象,如图所示.由图象不难看出,它们有2个交点.
所以方程sinx=
在[-π,π]内有2个解.
 解:函数y=sinx与y=
解:函数y=sinx与y=| 1 |
| x |
在同一坐标系内作出两个函数y=sinx,y=
| 1 |
| x |
所以方程sinx=
| 1 |
| x |
点评:本题考查正弦函数的图象,函数的零点与对应方程根的联系,重点锻炼了转化的数学思想.

练习册系列答案
相关题目
 四棱柱ABCD-A1B1C1D1的侧楞AA1垂直于底面,底面ABCD为直角梯形,AD∥BC,AD⊥AB,AD=AB=AA1=2BC,E为DD1的中点,F为A1D的中点.
四棱柱ABCD-A1B1C1D1的侧楞AA1垂直于底面,底面ABCD为直角梯形,AD∥BC,AD⊥AB,AD=AB=AA1=2BC,E为DD1的中点,F为A1D的中点.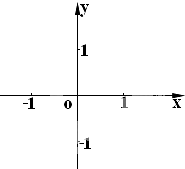 已知函数f(x)=
已知函数f(x)=