题目内容
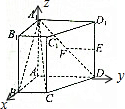
 四棱柱ABCD-A1B1C1D1的侧楞AA1垂直于底面,底面ABCD为直角梯形,AD∥BC,AD⊥AB,AD=AB=AA1=2BC,E为DD1的中点,F为A1D的中点.
四棱柱ABCD-A1B1C1D1的侧楞AA1垂直于底面,底面ABCD为直角梯形,AD∥BC,AD⊥AB,AD=AB=AA1=2BC,E为DD1的中点,F为A1D的中点.(1)求证:EF∥平面A1BC;
(2)求直线EF与平面A1CD所成角θ的正弦值.
考点:直线与平面所成的角,直线与平面平行的判定
专题:综合题,空间位置关系与距离,空间角
分析:(1)EF是△DA1C的中位线,得到EF∥A1C,从而证得EF∥平面A1BC.
(2)建立坐标系,设BC=1,则A1(0,0,2),C(2,1,0),D(0,2,0),E(0,2,1),F(0,1,1),求出平面A1CD的法向量,
,利用向量的夹角公式,即可求直线EF与平面A1CD所成角θ的正弦值.
(2)建立坐标系,设BC=1,则A1(0,0,2),C(2,1,0),D(0,2,0),E(0,2,1),F(0,1,1),求出平面A1CD的法向量,
| EF |
解答:
(1)证明:∵E为DD1的中点,F为A1D的中点,
∴EF是△DA1C的中位线,∴EF∥A1C.
∵A1C?面A1BC,EF?面A1BC,
∴EF∥平面A1BC.
(2)解:建立如图所示的坐标系,设BC=1,则A1(0,0,2),C(2,1,0),D(0,2,0),E(0,2,1),F(0,1,1),
∴
=(0,-1,0),
=(2,1,-2),
=(0,2,-2),
设平面A1CD的法向量为
=(x,y,z),则
,取
=(1,2,2),
∴直线EF与平面A1CD所成角θ的正弦值为
=
.
∴EF是△DA1C的中位线,∴EF∥A1C.
∵A1C?面A1BC,EF?面A1BC,
∴EF∥平面A1BC.
(2)解:建立如图所示的坐标系,设BC=1,则A1(0,0,2),C(2,1,0),D(0,2,0),E(0,2,1),F(0,1,1),

∴
| EF |
| A1C |
| A1D |
设平面A1CD的法向量为
| n |
|
| n |
∴直线EF与平面A1CD所成角θ的正弦值为
| 2 | ||||
|
| 2 |
| 3 |
点评:本题考查证明线面平行的方法,考查直线EF与平面A1CD所成角θ的正弦值,考查向量法的运用,属于中档题.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
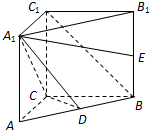 如图,在直三棱柱ABC-A1B1C1中,∠ACB=
如图,在直三棱柱ABC-A1B1C1中,∠ACB=