题目内容
已知在数列{an}中,a1=
,an=
an-1+
•
(n∈N+,n≥2).
(1)证明:数列{an+
}是等比数列;
(2)求数列{an}的通项公式.
| 1 |
| 6 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3n |
(1)证明:数列{an+
| 1 |
| 3n |
(2)求数列{an}的通项公式.
考点:等比关系的确定,数列递推式
专题:等差数列与等比数列
分析:(1)原式转化为an+
=
(an-1+
),再求出a1+
=
,继而得以证明,
(2)由(1)可知an+
=
×(
)n-1=(
)n,整理化简得到an=(
)n-
=
-
,需要验证a1成立
| 1 |
| 3n |
| 1 |
| 2 |
| 1 |
| 3n-1 |
| 1 |
| 3 |
| 1 |
| 2 |
(2)由(1)可知an+
| 1 |
| 3n |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3n |
| 1 |
| 2n |
| 1 |
| 3n |
解答:
解:(1)证明∵an=
an-1+
•
,
∴an+
=
(an-1+
),
∴a1+
=
+
=
,
故数列{an+
}是以
为首项,以
为公比的等比数列;
(2)由(1)可知an+
=
×(
)n-1=(
)n,
所以an=(
)n-
=
-
,
验证a1=
-
=
成立,
故以an=
-
.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3n |
∴an+
| 1 |
| 3n |
| 1 |
| 2 |
| 1 |
| 3n-1 |
∴a1+
| 1 |
| 3 |
| 1 |
| 6 |
| 1 |
| 3 |
| 1 |
| 2 |
故数列{an+
| 1 |
| 3n |
| 1 |
| 2 |
| 1 |
| 2 |
(2)由(1)可知an+
| 1 |
| 3n |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
所以an=(
| 1 |
| 2 |
| 1 |
| 3n |
| 1 |
| 2n |
| 1 |
| 3n |
验证a1=
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 6 |
故以an=
| 1 |
| 2n |
| 1 |
| 3n |
点评:本题考查了等比数列的定义和通项公式,属于基础题

练习册系列答案
相关题目
函数y=sin(3x+
)的图象的一条对称轴是( )
| 3π |
| 4 |
A、x=-
| ||
B、x=-
| ||
C、x=
| ||
D、x=-
|
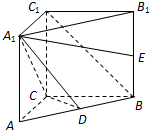 如图,在直三棱柱ABC-A1B1C1中,∠ACB=
如图,在直三棱柱ABC-A1B1C1中,∠ACB=