题目内容
已知在△ABC中,cosAtanA=-3
,求△ABC的形状.
| sinB |
| tanB |
考点:余弦定理
专题:解三角形
分析:根据△ABC中,各内角都大于0且小于π,结合题意,判断出△ABC的形状.
解答:
解:在△ABC中,∵cosAtanA=-3
,
∴cosA•
=-3•
,
∴sinA=-3cosB;
又∵A、B∈(0,π),
∴0<sinA≤1,
∴cosB<0,
∴
<B<π,
∴△ABC是钝角三角形.
| sinB |
| tanB |
∴cosA•
| sinA |
| cosA |
| sinB | ||
|
∴sinA=-3cosB;
又∵A、B∈(0,π),
∴0<sinA≤1,
∴cosB<0,
∴
| π |
| 2 |
∴△ABC是钝角三角形.
点评:本题考查了判断三角形的形状的问题,解题时应化简三角恒等式,根据角的取值范围,得出结论,是基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
若点(-1,m)在直线x+2y-1=0的上方,则y=
( )
| m2+1 |
| m-1 |
A、有最小值2+2
| ||
B、有最大值2+2
| ||
C、有最大值2-2
| ||
D、有最小值2
|
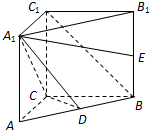 如图,在直三棱柱ABC-A1B1C1中,∠ACB=
如图,在直三棱柱ABC-A1B1C1中,∠ACB=