题目内容
若关于x的方程lg(-x2+mx-1)=lg(3-x)有两个不同的正数解,求实数m的取值范围.
考点:函数的零点
专题:函数的性质及应用
分析:根据对数函数得出不等式m>x+
,0<x<3有解,m≥2;再根据函数y=m,与函数y=x+
-1,有2个交点,得出3<m<
,总结即可得出实数m的取值范围.
| 1 |
| x |
| 4 |
| x |
| 10 |
| 3 |
解答:
解:∵关于x的方程lg(-x2+mx-1)=lg(3-x)有两个不同的正数解,
x<3,-x2+mx-1>0,
∴m=x+
-1有两个不同的正数解,且满足x<3,-x2+mx-1>0,
即不等式m>x+
,0<x<3有解,
∴m≥2
∵函数y=m,与函数y=x+
-1,有2个交点,
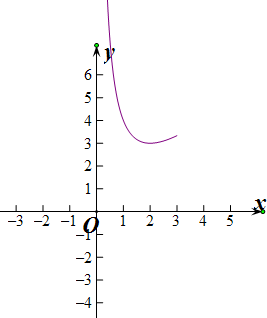
当x=2时,x+
最小值为4,当x=3时,x+
的值为3+
=
当x=2时,x+
-1≥3,当x=3时,x+
-1=
-1=
∴3<m<
,
综上:实数m的取值范围(3,
)
x<3,-x2+mx-1>0,
∴m=x+
| 4 |
| x |
即不等式m>x+
| 1 |
| x |
∴m≥2
∵函数y=m,与函数y=x+
| 4 |
| x |
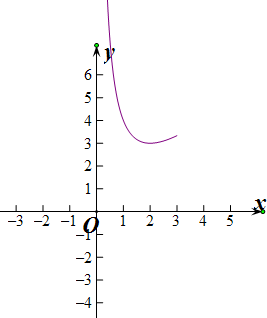
当x=2时,x+
| 4 |
| x |
| 4 |
| x |
| 4 |
| 3 |
| 13 |
| 3 |
当x=2时,x+
| 4 |
| x |
| 4 |
| x |
| 13 |
| 3 |
| 10 |
| 3 |
∴3<m<
| 10 |
| 3 |
综上:实数m的取值范围(3,
| 10 |
| 3 |
点评:本题综合考察了对数函数的性质,方程的根与函数图象的交点,运用数形结合的思想解决问题,难度较大.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
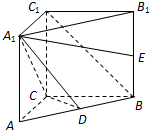 如图,在直三棱柱ABC-A1B1C1中,∠ACB=
如图,在直三棱柱ABC-A1B1C1中,∠ACB=