题目内容
5.已知函数f(x)=2cos(ωx+$\frac{3}{2}$π)(ω>0)的最小正周期为2π,则函数f(x)图象的一条对称轴方程为( )| A. | x=$\frac{π}{4}$ | B. | x=$\frac{π}{2}$ | C. | x=$\frac{3}{4}$π | D. | x=π |
分析 通过函数的周期,可求出ω,然后求出函数的对称轴方程,即可得到选项.
解答 解:函数f(x)=2cos(ωx+$\frac{3}{2}$π)(ω>0)的最小正周期为2π,
所以ω=1,函数f(x)=2cos(x+$\frac{3}{2}$π)=2sinx,
它的对称轴为:x=kπ+$\frac{π}{2}$,k∈Z,
当k=0时,可得,x=$\frac{π}{2}$,显然B正确.
故选:B.
点评 本题主要考查三角函数的周期公式的应用,及由正弦函数的性质求解函数的对称轴解析式的求法,对称轴方程的求法,考查计算能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.已知实数x,y满足$\left\{\begin{array}{l}{3x-y-7≥0}\\{5x-4y≤0}\\{y≤10}\end{array}\right.$,则$\frac{y+x}{x}$的最大值为( )
| A. | 1 | B. | $\frac{30}{17}$ | C. | $\frac{47}{17}$ | D. | 2 |
17.已知函数$f(x)=sin(ωx+\frac{π}{6})(ω>0)$的最小正周期为4π,则( )
| A. | 函数f(x)的图象关于原点对称 | |
| B. | 函数f(x)的图象关于直线$x=\frac{π}{3}$对称 | |
| C. | 函数f(x)图象上的所有点向右平移$\frac{π}{3}$个单位长度后,所得的图象关于原点对称 | |
| D. | 函数f(x)在区间(0,π)上单调递增 |
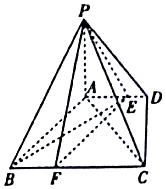 如图,四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD是直角梯形,∠ADC=90°,AD∥BC,AB⊥AC,AB=AC=$\sqrt{2}$,点E在AD上,且AE=2ED.
如图,四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD是直角梯形,∠ADC=90°,AD∥BC,AB⊥AC,AB=AC=$\sqrt{2}$,点E在AD上,且AE=2ED.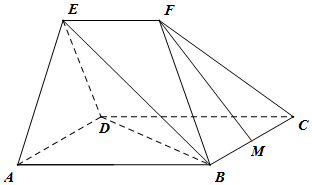 如图,在几何体ABCDEF中,平面ADE⊥平面ABCD,四边形ABCD为菱形,且∠DAB=60°,EA=ED=AB=2EF,EF∥AB,M为BC中点.
如图,在几何体ABCDEF中,平面ADE⊥平面ABCD,四边形ABCD为菱形,且∠DAB=60°,EA=ED=AB=2EF,EF∥AB,M为BC中点.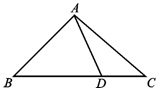 在△ABC中,角A,B,C所对的边分别为a,b,c,满足$\frac{{\sqrt{2}c-a}}{cosA}=\frac{b}{cosB}$,D是BC边上的一点.
在△ABC中,角A,B,C所对的边分别为a,b,c,满足$\frac{{\sqrt{2}c-a}}{cosA}=\frac{b}{cosB}$,D是BC边上的一点.