题目内容
10.若等比数列{an}的各项均为正数,且a3-a1=2,则a5的最小值为8.分析 由已知把首项用公比q表示,再由等比数列的通项公式可得a5,然后利用配方法求得a5的最小值.
解答 解:∵an>0,且a3-a1=2,
∴${a}_{1}{q}^{2}-{a}_{1}=2$,则${a}_{1}=\frac{2}{{q}^{2}-1}$(q>0),
∴${a}_{5}={a}_{1}{q}^{4}=\frac{2{q}^{4}}{{q}^{2}-1}$=$\frac{2}{\frac{1}{{q}^{2}}-\frac{1}{{q}^{4}}}$.
令$t=\frac{1}{{q}^{2}}$(t>0),则${a}_{5}=\frac{2}{-{t}^{2}+t}$,
又$-{t}^{2}+t=-(t-\frac{1}{2})^{2}+\frac{1}{4}≤\frac{1}{4}$,
∴a5∈[8,+∞).
∴a5的最小值为8.
故答案为:8.
点评 本题考查等比数列的通项公式,考查了利用配方法求函数的最值,是中档题.

练习册系列答案
相关题目
1.已知x,y∈R,那么“x>y”的充分必要条件是( )
| A. | 2x>2y | B. | lgx>lgy | C. | $\frac{1}{x}>\frac{1}{y}$ | D. | x2>y2 |
5.已知流程图如图所示,该程序运行后,为使输出的f(x)值为16,则循环体的判断框内①处应( )
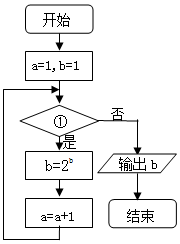

| A. | a>3? | B. | a≥3? | C. | a≤3? | D. | a<3? |
7. 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<$\frac{π}{2}$)的图象(部分)如图所示,则f(x)的解析式是( )
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<$\frac{π}{2}$)的图象(部分)如图所示,则f(x)的解析式是( )
 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<$\frac{π}{2}$)的图象(部分)如图所示,则f(x)的解析式是( )
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<$\frac{π}{2}$)的图象(部分)如图所示,则f(x)的解析式是( )| A. | f(x)=2sin(πx+$\frac{π}{6}$) | B. | f(x)=2sin(2πx+$\frac{π}{6}$) | C. | f(x)=2sin(πx+$\frac{π}{3}$) | D. | f(x)=2sin(2πx+$\frac{π}{3}$) |
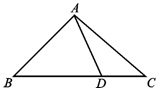 在△ABC中,角A,B,C所对的边分别为a,b,c,满足$\frac{{\sqrt{2}c-a}}{cosA}=\frac{b}{cosB}$,D是BC边上的一点.
在△ABC中,角A,B,C所对的边分别为a,b,c,满足$\frac{{\sqrt{2}c-a}}{cosA}=\frac{b}{cosB}$,D是BC边上的一点.