题目内容
6.已知双曲线G以原点O为中心,过$(\sqrt{5},\;4)$点,且以抛物线C:y2=4x的焦点为右顶点,那么双曲线G的方程为${x^2}-\frac{y^2}{4}=1$.分析 根据题意,由抛物线方程可得其焦点坐标,即可得双曲线G的右顶点坐标,分析可得双曲线的焦点位置以及a的值,可以设其方程为:x2-$\frac{{y}^{2}}{{b}^{2}}$=1,将点$(\sqrt{5},\;4)$坐标代入双曲线方程可得4-$\frac{4}{{b}^{2}}$=1,解可得b2的值,将b2的值代入双曲线的方程,即可得答案.
解答 解:根据题意,抛物线C:y2=4x的焦点为(1,0),
即双曲线G的右顶点坐标为(1,0),
则该双曲线的焦点在x轴上,且其中a=1,设其方程为:x2-$\frac{{y}^{2}}{{b}^{2}}$=1,
又由双曲线过点$(\sqrt{5},\;4)$,
则有5-$\frac{4}{{b}^{2}}$=1,解可得b2=4,
则双曲线G的方程为${x^2}-\frac{y^2}{4}=1$;
故答案为:${x^2}-\frac{y^2}{4}=1$.
点评 本题考查双曲线的几何性质,关键是有抛物线的方程确定其焦点坐标,确定双曲线的右顶点坐标.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
17.已知函数$f(x)=sin(ωx+\frac{π}{6})(ω>0)$的最小正周期为4π,则( )
| A. | 函数f(x)的图象关于原点对称 | |
| B. | 函数f(x)的图象关于直线$x=\frac{π}{3}$对称 | |
| C. | 函数f(x)图象上的所有点向右平移$\frac{π}{3}$个单位长度后,所得的图象关于原点对称 | |
| D. | 函数f(x)在区间(0,π)上单调递增 |
1.已知x,y∈R,那么“x>y”的充分必要条件是( )
| A. | 2x>2y | B. | lgx>lgy | C. | $\frac{1}{x}>\frac{1}{y}$ | D. | x2>y2 |
3.已知函数f(x)=asinx+bcosx(a≠0)在$x=\frac{π}{4}$处取得最小值,则函数$f(\frac{3π}{4}-x)$是( )
| A. | 偶函数且它的图象关于点(π,0)对称 | |
| B. | 偶函数且它的图象关于点$(\frac{3π}{2},0)$对称 | |
| C. | 奇函数且它的图象关于点(π,0)对称 | |
| D. | 奇函数且它的图象关于点$(\frac{3π}{2},0)$对称 |
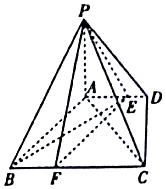 如图,四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD是直角梯形,∠ADC=90°,AD∥BC,AB⊥AC,AB=AC=$\sqrt{2}$,点E在AD上,且AE=2ED.
如图,四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD是直角梯形,∠ADC=90°,AD∥BC,AB⊥AC,AB=AC=$\sqrt{2}$,点E在AD上,且AE=2ED.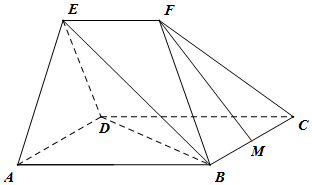 如图,在几何体ABCDEF中,平面ADE⊥平面ABCD,四边形ABCD为菱形,且∠DAB=60°,EA=ED=AB=2EF,EF∥AB,M为BC中点.
如图,在几何体ABCDEF中,平面ADE⊥平面ABCD,四边形ABCD为菱形,且∠DAB=60°,EA=ED=AB=2EF,EF∥AB,M为BC中点.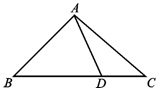 在△ABC中,角A,B,C所对的边分别为a,b,c,满足$\frac{{\sqrt{2}c-a}}{cosA}=\frac{b}{cosB}$,D是BC边上的一点.
在△ABC中,角A,B,C所对的边分别为a,b,c,满足$\frac{{\sqrt{2}c-a}}{cosA}=\frac{b}{cosB}$,D是BC边上的一点.