题目内容
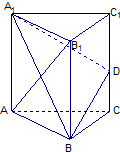 如图,已知三棱柱ABC-A1B1C1的所有棱长都相等,且侧棱垂直于底面,由B沿棱柱侧面经过棱CC1到点A1的最短路线长为2
如图,已知三棱柱ABC-A1B1C1的所有棱长都相等,且侧棱垂直于底面,由B沿棱柱侧面经过棱CC1到点A1的最短路线长为2| 5 |
(1)求三棱柱ABC-A1B1C1的棱长;
(2)求四棱锥A1-BCC1B1的体积;
(3)在平面A1BD内是否存在过点D的直线与平面ABC平行?并说明理由.
考点:直线与平面平行的判定,棱柱、棱锥、棱台的体积,点、线、面间的距离计算
专题:空间位置关系与距离
分析:(1)把三棱柱沿AA1剪开,并展开如图所示,则BE=2
,设棱长为a,在Rt△BEF中,4a2+a2=20,所以求得a=2;
(2)过A1作B1C1的垂线A1G,则容易说明A1G就是四棱锥A1-BCC1B12高,所以根据四棱锥的体积公式即可求该四棱锥的体积;
(3)取A1C的中点H,取A1B的中点O,依次连接DH,HO,OD,则容易说明OD就是所找直线.
| 5 |
(2)过A1作B1C1的垂线A1G,则容易说明A1G就是四棱锥A1-BCC1B12高,所以根据四棱锥的体积公式即可求该四棱锥的体积;
(3)取A1C的中点H,取A1B的中点O,依次连接DH,HO,OD,则容易说明OD就是所找直线.
解答:
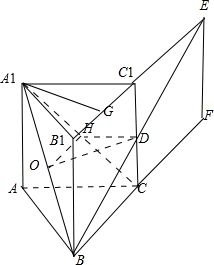 解:(1)将三棱柱沿AA1剪开并展开和平面BCC1B1重合,如图所示,A1点变成了E点,连接AE,与CC1的交点就是D点,线段BE的长便是B到A1的最短距离;
解:(1)将三棱柱沿AA1剪开并展开和平面BCC1B1重合,如图所示,A1点变成了E点,连接AE,与CC1的交点就是D点,线段BE的长便是B到A1的最短距离;
∴BE=2
,设三棱柱的棱长为a,则:由图可知,(2a)2+a2=(2
)2,∴a=2;
即三棱柱ABC-A1B1C1的棱长为2;
(2)过A1作A1G⊥B1C1,垂足为G,∵侧棱垂直于底面,∴BB1⊥A1G,即A1G⊥BB1,又A1G⊥B1C1;
∴A1G⊥平面BCC1B1,即A1G是四棱锥A1-BCC1B1的底面上的高,且A1G=
,S底面BCC1B1=4;
∴四棱锥A1-BCC1B1的体积V=
;
(3)连接A1C,取A1C的中点H,连接DH,∵D是CC1的中点,∴DH∥AC,AC?平面ABC,DH?平面ABC,∴DH∥平面ABC;
取A1B的中点O,连接HO,则HO∥BC,BC?平面ABC,∴OH∥平面ABC,HO∩DH=H;
∴平面DHO∥平面ABC,连接OD,则OD∥平面ABC;
即在平面A1BD内存在过点D的直线OD与平面ABC平行.
 解:(1)将三棱柱沿AA1剪开并展开和平面BCC1B1重合,如图所示,A1点变成了E点,连接AE,与CC1的交点就是D点,线段BE的长便是B到A1的最短距离;
解:(1)将三棱柱沿AA1剪开并展开和平面BCC1B1重合,如图所示,A1点变成了E点,连接AE,与CC1的交点就是D点,线段BE的长便是B到A1的最短距离;∴BE=2
| 5 |
| 5 |
即三棱柱ABC-A1B1C1的棱长为2;
(2)过A1作A1G⊥B1C1,垂足为G,∵侧棱垂直于底面,∴BB1⊥A1G,即A1G⊥BB1,又A1G⊥B1C1;
∴A1G⊥平面BCC1B1,即A1G是四棱锥A1-BCC1B1的底面上的高,且A1G=
| 3 |
∴四棱锥A1-BCC1B1的体积V=
4
| ||
| 3 |
(3)连接A1C,取A1C的中点H,连接DH,∵D是CC1的中点,∴DH∥AC,AC?平面ABC,DH?平面ABC,∴DH∥平面ABC;
取A1B的中点O,连接HO,则HO∥BC,BC?平面ABC,∴OH∥平面ABC,HO∩DH=H;
∴平面DHO∥平面ABC,连接OD,则OD∥平面ABC;
即在平面A1BD内存在过点D的直线OD与平面ABC平行.
点评:考查线面垂直的性质,线面垂直的判定定理,线面平行的判定定理,面面平行的判定定理.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知AB∥PQ,BC∥QR,∠ABC=30°,则∠PQR等于( )
| A、30° |
| B、300或1500 |
| C、1500 |
| D、以上都不对 |