题目内容
已知函数f(x)=
,若f(1)=2.
(1)求实数a的值;
(2)若f(x)=3,求x的值;
(3)画出函数的图象说出函数f(x)的值域(不必写出过程).
|
(1)求实数a的值;
(2)若f(x)=3,求x的值;
(3)画出函数的图象说出函数f(x)的值域(不必写出过程).
考点:二次函数的性质
专题:函数的性质及应用
分析:(1)根据f(x)的解析式,需将1带入f(x)=ax2+1中,f(1)=a+1=2,所以a=1;
(2)将f(x)=3带入f(x)=x2+1,x>0,中,从而求出x;
(3)画出函数f(x)的图象,根据图象即可说出f(x)的值域.
(2)将f(x)=3带入f(x)=x2+1,x>0,中,从而求出x;
(3)画出函数f(x)的图象,根据图象即可说出f(x)的值域.
解答:
解:(1)f(1)=a+1=2,∴a=1;
(2)f(x)=
;
∵f(x)=3,∴x2+1=3,x>0,∴解得x=
;
(3)由图象可以看出函数f(x)的值域为(-∞,-1]∪(1,+∞).

(2)f(x)=
|
∵f(x)=3,∴x2+1=3,x>0,∴解得x=
| 2 |
(3)由图象可以看出函数f(x)的值域为(-∞,-1]∪(1,+∞).

点评:考查根据条件求分段函数解析式,注意每一段x的取值,在已知函数值求自变量值时要判断带入那一段函数中,画分段函数的图象以及根据图象求函数的值域.

练习册系列答案
相关题目
下列命题是真命题的是( )
①“若x2+y2≠0,则x,y不全为零”的否命题;
②“正六边形都相似”的逆命题;
③“若m>0,则x2+x-m=0有实根”的逆否命题;
④“若x-3
是有理数,则x是无理数”
①“若x2+y2≠0,则x,y不全为零”的否命题;
②“正六边形都相似”的逆命题;
③“若m>0,则x2+x-m=0有实根”的逆否命题;
④“若x-3
| 1 |
| 2 |
| A、①④ | B、③④ |
| C、①③④ | D、①②③④ |
已知集合M={y|y=2x,x∈R},N={x|y=2x,x∈R},则M∩N=( )
| A、∅ | B、[0,+∞) |
| C、(0,+∞) | D、R |
已知P(x0,y0)是抛物线y2=2px(p>0)上的一点,过P点的切线方程的斜率可通过如下方式求得:在y2=2px两边同时对x求导,得2yy′=2p,则y′=
,所以过P的切线的斜率:k=
,试用上述方法求出椭圆
+y2=1在P(1,
)处的切线方程为( )
| p |
| y |
| p |
| y0 |
| x2 |
| 4 |
| ||
| 2 |
A、x-2
| ||
B、x+2
| ||
C、x-2
| ||
D、x+2
|
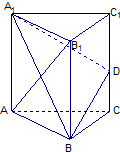 如图,已知三棱柱ABC-A1B1C1的所有棱长都相等,且侧棱垂直于底面,由B沿棱柱侧面经过棱CC1到点A1的最短路线长为2
如图,已知三棱柱ABC-A1B1C1的所有棱长都相等,且侧棱垂直于底面,由B沿棱柱侧面经过棱CC1到点A1的最短路线长为2