题目内容
给出下列命题:
①命题“?x∈R,x2+x+1>0的否定是:?x∈R,x2+x=1<0;
②命题“若ab=0,则a=0或b=0”的否命题是“若ab≠0,则a≠0且b≠0”;
③?x、y∈R,sin(x-y)=sinx-siny;
④向量
,
均是单位向量,其夹角为θ,则命题“p:|
-
|>1”是命题“q:θ∈[
,
]”的充要条件.其中正确的命题的个数是( )
①命题“?x∈R,x2+x+1>0的否定是:?x∈R,x2+x=1<0;
②命题“若ab=0,则a=0或b=0”的否命题是“若ab≠0,则a≠0且b≠0”;
③?x、y∈R,sin(x-y)=sinx-siny;
④向量
| a |
| b |
| a |
| b |
| π |
| 2 |
| 5π |
| 6 |
| A、4 | B、3 | C、2 | D、1 |
考点:命题的真假判断与应用
专题:简易逻辑
分析:①写出命题“?x∈R,x2+x+1>0的否定,可判断①的正误;
②写出命题“若ab=0,则a=0或b=0”的否命题,可判断②的正误;
③③?x=y=0∈R,sin(0-0)=sin0-sin0=0,可判断③的正误;
④由p:|
-
|>1⇒θ∈(
,π],从而可判断④的正误.
②写出命题“若ab=0,则a=0或b=0”的否命题,可判断②的正误;
③③?x=y=0∈R,sin(0-0)=sin0-sin0=0,可判断③的正误;
④由p:|
| a |
| b |
| π |
| 3 |
解答:
解:①命题“?x∈R,x2+x+1>0的否定是:?x∈R,x2+x=1≤0,①错误;
②命题“若ab=0,则a=0或b=0”的否命题是“若ab≠0,则a≠0且b≠0”,②正确;
③?x=y=0∈R,sin(0-0)=sin0-sin0=0,③正确;
④向量
,
均是单位向量,其夹角为θ,则命题“p:|
-
|>1”,
所以,|
-
|2=
2+
2-2
•
>1,即1+1-2×1×1×cosθ>1,
所以,cosθ<
,又θ∈[0,π],所以θ∈(
,π];
命题“q:θ∈[
,
]”,显然命题p不能⇒命题q,即充分性不成立,故④错误;
综上所述,正确的命题的个数2个,
故选:C.
②命题“若ab=0,则a=0或b=0”的否命题是“若ab≠0,则a≠0且b≠0”,②正确;
③?x=y=0∈R,sin(0-0)=sin0-sin0=0,③正确;
④向量
| a |
| b |
| a |
| b |
所以,|
| a |
| b |
| a |
| b |
| a |
| b |
所以,cosθ<
| 1 |
| 2 |
| π |
| 3 |
命题“q:θ∈[
| π |
| 2 |
| 5π |
| 6 |
综上所述,正确的命题的个数2个,
故选:C.
点评:本题考查命题的真假判断与应用,综合考查命题的否定、否命题及特称命题、充分必要条件的判断的应用,属于中档题.

练习册系列答案
相关题目
函数f(x)=x3-ax2+x在x=1处的切线与直线x+2y-3=0垂直,则a的值为( )
| A、3 | B、2 | C、1 | D、-1 |
已知P(x0,y0)是抛物线y2=2px(p>0)上的一点,过P点的切线方程的斜率可通过如下方式求得:在y2=2px两边同时对x求导,得2yy′=2p,则y′=
,所以过P的切线的斜率:k=
,试用上述方法求出椭圆
+y2=1在P(1,
)处的切线方程为( )
| p |
| y |
| p |
| y0 |
| x2 |
| 4 |
| ||
| 2 |
A、x-2
| ||
B、x+2
| ||
C、x-2
| ||
D、x+2
|
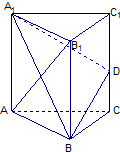 如图,已知三棱柱ABC-A1B1C1的所有棱长都相等,且侧棱垂直于底面,由B沿棱柱侧面经过棱CC1到点A1的最短路线长为2
如图,已知三棱柱ABC-A1B1C1的所有棱长都相等,且侧棱垂直于底面,由B沿棱柱侧面经过棱CC1到点A1的最短路线长为2 某城市理论预测2000年到2004年人口总数与年份的关系如下表所示:
某城市理论预测2000年到2004年人口总数与年份的关系如下表所示:
