题目内容
某地人民医院急诊科2011年的住院病人数y(人)是时间t(1≤t≤12,t∈N*,单位:月)的函数,根据资料有如下统计数据:
y与t函数可以近似的看成正弦函数y=Asin(ωt+φ)+b(A,ω,φ,b为正常数且0<φ<π).
(1)求函数的解析式;
(2)根据所得函数解析式估计一年中大约有几个月的时间急诊科的住院病人数大于或等于35人.
| t | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| y | 40 | 37 | 33 | 30 | 27 | 24 | 20 | 23 | 26 | 31 | 34 | 36 |
(1)求函数的解析式;
(2)根据所得函数解析式估计一年中大约有几个月的时间急诊科的住院病人数大于或等于35人.
考点:在实际问题中建立三角函数模型
专题:综合题,三角函数的图像与性质
分析:(1)先求出b,利用最多的月为40人,最少的月为20人,求出A,再求出ω=
,φ=
,即可求函数的解析式;
(2)10sin(
t+
)+30≥35,求出t的范围,即可得出结论.
| π |
| 6 |
| π |
| 3 |
(2)10sin(
| π |
| 6 |
| π |
| 3 |
解答:
解:(1)一年总人数为361人,平均每月为361/12=30人,b=30,
最多的月为40人,最少的月为20人,相差20人,此为正弦函数的最大值和最小值之差,即2A=20,A=10,
t=1,正弦函数取最大值:ωt+φ=ω+φ=
=7,正弦函数取最小值:ωt+φ=7ω+φ=
,
解得ω=
,φ=
,
∴y=10sin(
t+
)+30;
(2)10sin(
t+
)+30≥35,
∴sin(
t+
)≥
,
∴
≤
t+
≤
,
∴-2≤t≤2,
∴t=-2,-1,1,2,分别相当于11,12,1,2月 (0无意义),每年约有4个月内住院人数大于或等于35人.
最多的月为40人,最少的月为20人,相差20人,此为正弦函数的最大值和最小值之差,即2A=20,A=10,
t=1,正弦函数取最大值:ωt+φ=ω+φ=
| π |
| 2t |
| 3π |
| 2 |
解得ω=
| π |
| 6 |
| π |
| 3 |
∴y=10sin(
| π |
| 6 |
| π |
| 3 |
(2)10sin(
| π |
| 6 |
| π |
| 3 |
∴sin(
| π |
| 6 |
| π |
| 3 |
| 1 |
| 2 |
∴
| π |
| 6 |
| π |
| 6 |
| π |
| 3 |
| 5π |
| 6 |
∴-2≤t≤2,
∴t=-2,-1,1,2,分别相当于11,12,1,2月 (0无意义),每年约有4个月内住院人数大于或等于35人.
点评:本题考查在实际问题中建立三角函数模型,考查学生利用数学知识解决实际问题,属于中档题.

练习册系列答案
相关题目
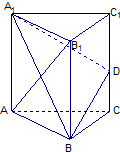 如图,已知三棱柱ABC-A1B1C1的所有棱长都相等,且侧棱垂直于底面,由B沿棱柱侧面经过棱CC1到点A1的最短路线长为2
如图,已知三棱柱ABC-A1B1C1的所有棱长都相等,且侧棱垂直于底面,由B沿棱柱侧面经过棱CC1到点A1的最短路线长为2