题目内容
求下列函数的定义域:
(1)y=
•
;
(2)y=
.
(1)y=
| x-2 |
| x+5 |
(2)y=
| ||
| |x|-5 |
考点:函数的定义域及其求法
专题:函数的性质及应用
分析:根据函数成立的条件,即可得到结论.
解答:
解:(1)要使函数f(x)有意义,则
,即
,解得x≥2,故函数的定义域为[2,+∞).
(2)要使函数f(x)有意义,则
,即
,解得x≥4且x≠5,故函数的定义域为{x|x≥4且x≠5}.
|
|
(2)要使函数f(x)有意义,则
|
|
点评:本题主要考查函数的定义域的求解,要求熟练掌握常见函数成立的条件.

练习册系列答案
相关题目
已知集合M={y|y=2x,x∈R},N={x|y=2x,x∈R},则M∩N=( )
| A、∅ | B、[0,+∞) |
| C、(0,+∞) | D、R |
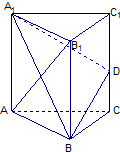 如图,已知三棱柱ABC-A1B1C1的所有棱长都相等,且侧棱垂直于底面,由B沿棱柱侧面经过棱CC1到点A1的最短路线长为2
如图,已知三棱柱ABC-A1B1C1的所有棱长都相等,且侧棱垂直于底面,由B沿棱柱侧面经过棱CC1到点A1的最短路线长为2