题目内容
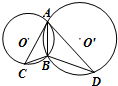如图，圆O与圆O′相交于A、B两点，AD与AC分别是圆O与圆O′的A点处的切线．若BD=2BC=2，则AB=考点：相似三角形的性质
专题：直线与圆
分析：由已知条件条件出△ACB∽△DAB，从而得到AB2=BC×BD，由此能求出AB；由∠CAB=30°，得到∠COB=2∠CAB=60°．
解答：
解：∵AC是⊙O'的切线
∴∠CAB=∠D（弦切角等于它夹弧所对的圆周角）
∵AD是⊙O的切线
∴∠DAB=∠C
∴△ACB∽△DAB，
∴
=
，
∴AB2=BC×BD=2，
∴AB=
；
∵∠CAB=30°，∴∠COB=2∠CAB=60°．
故答案为：
，60°．
∴∠CAB=∠D（弦切角等于它夹弧所对的圆周角）
∵AD是⊙O的切线
∴∠DAB=∠C
∴△ACB∽△DAB，
∴
| BC |
| AB |
| AB |
| BD |
∴AB2=BC×BD=2，
∴AB=
| 2 |
∵∠CAB=30°，∴∠COB=2∠CAB=60°．
故答案为：
| 2 |
点评：本题考查线段长的求法，考查角的大小的求法，解题时要认真审题，注意三角形相似的性质的合理运用．
练习册系列答案
备战中考寒假系列答案
相关题目
将一列有规律的正整数排成一个三角形数阵（如图）：根据排列规律，数阵中第12行的从左至右的第4个数是