题目内容
已知向量
，
夹角为60°，且|
|=1，|2
-
|=2
，则|
|= ．
| a |
| b |
| a |
| a |
| b |
| 3 |
| b |
考点：数量积表示两个向量的夹角,向量的模,平面向量数量积的运算
专题：平面向量及应用
分析：利用数量积运算和性质即可得出．
解答：
解：∵|2
-
|=2
，∴4
2-4
•
+
2=12，
∴4×12-4×1×|
|cos60°+|
|2=12，
化为|
|2-2|
|-8=0，
解得|
|=4．
故答案为：4．
| a |
| b |
| 3 |
| a |
| a |
| b |
| b |
∴4×12-4×1×|
| b |
| b |
化为|
| b |
| b |
解得|
| b |
故答案为：4．
点评：本题考查了数量积运算和性质，属于基础题．
练习册系列答案
相关题目
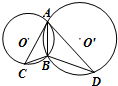如图，圆O与圆O′相交于A、B两点，AD与AC分别是圆O与圆O′的A点处的切线．若BD=2BC=2，则AB=