题目内容
 将一列有规律的正整数排成一个三角形数阵(如图):根据排列规律,数阵中第12行的从左至右的第4个数是
将一列有规律的正整数排成一个三角形数阵(如图):根据排列规律,数阵中第12行的从左至右的第4个数是考点:归纳推理
专题:规律型,推理和证明
分析:由图不的数据我们不难得到,图中的每一行的数据由小到大排列后,是一个以1为首项,以3为公差的等差数列,并且分析图中数据的排列情况,第一行1个数,第二行2个数,第三个3个数,…由此不难得到数的排列规律.
解答:
解:图中的每一行的数据由小到大排列后,
是一个以1为首项,以3为公差的等差数列{an},
则ak=3k-2(k∈N+)
由于图中,第一行1个数,第二行2个数,第三个3个数,…
∴前n-1行共有1+2+3+…+(n-1)=
个数据,
则第12行的从左至右的第4个数是数列{an}的第
+4=70项,
∵a59=3×70-2=208,
故答案为:208
是一个以1为首项,以3为公差的等差数列{an},
则ak=3k-2(k∈N+)
由于图中,第一行1个数,第二行2个数,第三个3个数,…
∴前n-1行共有1+2+3+…+(n-1)=
| n(n-1) |
| 2 |
则第12行的从左至右的第4个数是数列{an}的第
| 12×(12-1) |
| 2 |
∵a59=3×70-2=208,
故答案为:208
点评:归纳推理的一般步骤是:(1)通过观察个别情况发现某些相同性质;(2)从已知的相同性质中推出一个明确表达的一般性命题(猜想).

练习册系列答案
相关题目
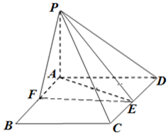 如图,P-AD-C是直二面角,四边形ABCD为菱形,且∠BAD=120°,AB=2,PA⊥AD,E是CD的中点,设PC与平面ABCD所成的角为45°.
如图,P-AD-C是直二面角,四边形ABCD为菱形,且∠BAD=120°,AB=2,PA⊥AD,E是CD的中点,设PC与平面ABCD所成的角为45°.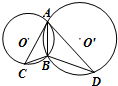 如图,圆O与圆O′相交于A、B两点,AD与AC分别是圆O与圆O′的A点处的切线.若BD=2BC=2,则AB=
如图,圆O与圆O′相交于A、B两点,AD与AC分别是圆O与圆O′的A点处的切线.若BD=2BC=2,则AB=