题目内容
在△ABC中，已知CA=2，CB=3，∠ACB=60°，CH为AB边上的高．设
=m
+n
其中m，n∈R，则
等于 ．
. |
| CH |
. |
| CB |
. |
| CA |
| m |
| n |
考点：向量在几何中的应用
专题：平面向量及应用
分析：因为CA，CB的边长及它们的夹角已知，所以可以
，
为基底，然后根据垂直或共线的条件列出关于m、n的方程，应该可以得到m，n的比值．
| CA |
| CB |
解答：
解：∵CA=2，CB=3，∠ACB=60°，
∴
•
=2×3×cos60°=3，
又∵CH为AB边上的高，∴
⊥
，设
=m
+n
其中m，n∈R，且
=
-
，
∴
•
=0，即（m
+n
）•(
-
)=0，
∴m
2+(n-m)
•
-n
2=0，
化简得n=6m，
∴
=
．
故答案为
．
∴
| CA |
| CB |
又∵CH为AB边上的高，∴
| CH |
| AB |
. |
| CH |
. |
| CB |
. |
| CA |
| AB |
| CB |
| CA |
∴
| CH |
| AB |
. |
| CB |
. |
| CA |
| CB |
| CA |
∴m
| CB |
| CB |
| CA |
| CA |
化简得n=6m，
∴
| m |
| n |
| 1 |
| 6 |
故答案为
| 1 |
| 6 |
点评：利用平面向量解决平面几何问题，往往先选定基底，然后把题目中涉及到的已知、所求的量用基底表示，然后借助于共线、垂直、角度、模长等条件列方程求解．
练习册系列答案
相关题目
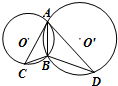如图，圆O与圆O′相交于A、B两点，AD与AC分别是圆O与圆O′的A点处的切线．若BD=2BC=2，则AB=