题目内容
7.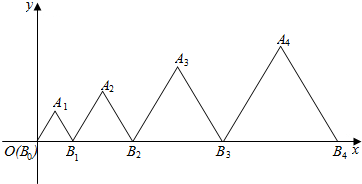 如图,在平面直角坐标系中,边长为an的一组正三角形AnBn-1Bn的底边Bn-1Bn依次排列在x轴上(B0与坐标原点重合).设{an}是首项为a,公差为d的等差数列,若所有正三角形顶点An在第一象限,且均落在抛物线y2=2px(p>0)上,则$\frac{a}{d}$的值为1.
如图,在平面直角坐标系中,边长为an的一组正三角形AnBn-1Bn的底边Bn-1Bn依次排列在x轴上(B0与坐标原点重合).设{an}是首项为a,公差为d的等差数列,若所有正三角形顶点An在第一象限,且均落在抛物线y2=2px(p>0)上,则$\frac{a}{d}$的值为1.
分析 根据题意得,正三角形A1B0B1的边长为a,利用正三角形的性质得出点A1的坐标,又点A1落在抛物线y2=2px(p>0)上,则点A1的坐标适合抛物线方程,得到p=$\frac{3}{4}$a;又{an}是首项为a,公差为d的等差数列,同理得到点A2的坐标且点A2落在抛物线y2=2px(p>0)上,则有a=d,从而求出答案.
解答 解:由题意得,正三角形A1B0B1的边长为a,
∴点A1的坐标为($\frac{a}{2}$,$\frac{\sqrt{3}a}{2}$),
又∵点A1落在抛物线y2=2px(p>0)上,则($\frac{\sqrt{3}a}{2}$)2=2p×$\frac{a}{2}$,
∴p=$\frac{3}{4}$a,
又{an}是首项为a,公差为d的等差数列,a2=a+d,
即正三角形A2B1B2的边长为a+d,
∴点A2的坐标为(a+$\frac{a+d}{2}$,$\frac{\sqrt{3}(a+d)}{2}$),
又∵点A2落在抛物线y2=2px(p>0)上,则[$\frac{\sqrt{3}(a+d)}{2}$]2=2p(a+$\frac{a+d}{2}$),
化简得(a-d)(2a+d)=0,∵2a+d>0,
∴a=d,
则$\frac{a}{d}$的值为1.
故答案为:1.
点评 本题主要考查数列与解析几何综合的知识点,本题是一道综合性的习题,解答本题的关键是准确求出正三角形的坐标后代入抛物线方程得出变量之间的关系式.

练习册系列答案
 目标测试系列答案
目标测试系列答案
相关题目
15.关于空间直角坐标系,下列叙述正确的是( )
| A. | P(x,y,z)中x,y,z的位置可以互换的 | |
| B. | 空间直角坐标系中的点与一个三元有序数组是一种一一对应关系 | |
| C. | 空间直角坐标系中的三条坐标轴把空间分成八个部分 | |
| D. | 某点在不同空间直角坐标系中的坐标位置可以相同 |
13.f(x)=$\left\{\begin{array}{l}{(3a-1)x+4a(x<1)}\\{{a}^{x}(x≥1)}\end{array}\right.$是定义在(-∞,+∞)上是减函数,则a的取值范围是( )
| A. | [$\frac{1}{6}$,$\frac{1}{3}$) | B. | (0,$\frac{1}{3}$) | C. | (0,$\frac{1}{6}$] | D. | ($\frac{1}{3}$,1) |
2.已知函数f(x)=3sinωxcosωx+$\sqrt{3}$cos2ωx(ω>0)的最小正周期为$\frac{π}{2}$,将函数f(x)的图象向左平移$\frac{π}{6}$个单位后,得到的函数g(x)=( )
| A. | $\sqrt{3}$cos4x+$\frac{\sqrt{3}}{2}$ | B. | -$\sqrt{3}$cos4x+$\frac{\sqrt{3}}{2}$ | C. | $\sqrt{3}$sin(4x+$\frac{5}{6}$π)+$\frac{\sqrt{3}}{2}$ | D. | $\sqrt{3}$sin(4x-$\frac{5}{6}$π)+$\frac{\sqrt{3}}{2}$ |
12.在△ABC中,C>$\frac{π}{2}$,若函数y=f(x)在[0,1]上为单调递减函数,则下列命题正确的是( )
| A. | f(cosA)>f(cosB) | B. | f(sinA)>f(sinB) | C. | f(sinA)>f(cosB) | D. | f(sinA)<f(cosB) |
19.已知复数z=3+$\frac{3-4i}{4+3i}$,则$\overline z$=( )
| A. | 3-i | B. | 2-3i | C. | 3+i | D. | 2+3i |
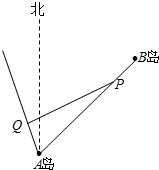 已知海岛B在海岛A的北偏东45°的方向上,两岛相距10海里.小船P从海岛B以2海里/小时的速度沿直线向海岛A移动,同时小船Q从海岛A出发,沿北偏西15°方向以4海里/小时的速度移动.
已知海岛B在海岛A的北偏东45°的方向上,两岛相距10海里.小船P从海岛B以2海里/小时的速度沿直线向海岛A移动,同时小船Q从海岛A出发,沿北偏西15°方向以4海里/小时的速度移动.