题目内容
2.已知函数f(x)=3sinωxcosωx+$\sqrt{3}$cos2ωx(ω>0)的最小正周期为$\frac{π}{2}$,将函数f(x)的图象向左平移$\frac{π}{6}$个单位后,得到的函数g(x)=( )| A. | $\sqrt{3}$cos4x+$\frac{\sqrt{3}}{2}$ | B. | -$\sqrt{3}$cos4x+$\frac{\sqrt{3}}{2}$ | C. | $\sqrt{3}$sin(4x+$\frac{5}{6}$π)+$\frac{\sqrt{3}}{2}$ | D. | $\sqrt{3}$sin(4x-$\frac{5}{6}$π)+$\frac{\sqrt{3}}{2}$ |
分析 由条件利用三角恒等变换化简函数的解析式,再利用正弦函数的周期性求得ω,再根据y=Asin(ωx+φ)的图象变换规律,得出结论.
解答 解:由于函数f(x)=3sinωxcosωx+$\sqrt{3}$cos2ωx=$\frac{3}{2}$sin2ωx+$\frac{\sqrt{3}}{2}$(1+cos2ωx)
=$\sqrt{3}$sin(2ωx+$\frac{π}{6}$)+$\frac{\sqrt{3}}{2}$ (ω>0)
的最小正周期为$\frac{2π}{2ω}$=$\frac{π}{2}$,ω=2,f(x)=$\sqrt{3}$sin(4x+$\frac{π}{6}$)+$\frac{\sqrt{3}}{2}$.
将函数f(x)的图象向左平移$\frac{π}{6}$个单位后,得到的函数g(x)=$\sqrt{3}$sin[4(x+$\frac{π}{6}$)+$\frac{π}{6}$]+$\frac{\sqrt{3}}{2}$
=$\sqrt{3}$sin(4x+$\frac{5π}{6}$)+$\frac{\sqrt{3}}{2}$,
故选:C.
点评 本题主要考查三角恒等变换,正弦函数的周期性,y=Asin(ωx+φ)的图象变换规律,属于中档题.

练习册系列答案
相关题目
10.已知△ABC中,a=4,b=5,A=30°.下列对三角形解的情况的判断中,正确的是( )
| A. | 一解 | B. | 两解 | C. | 无解 | D. | 一解或无解 |
11.log${\;}_{\sqrt{2}}$27×log${\;}_{\frac{1}{3}}$8=( )
| A. | 12 | B. | 18 | C. | -18 | D. | -$\frac{9}{2}$ |
11.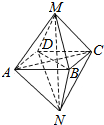 如图所示的几何体,关于其结构特征,下列说法不正确的是( )
如图所示的几何体,关于其结构特征,下列说法不正确的是( )
 如图所示的几何体,关于其结构特征,下列说法不正确的是( )
如图所示的几何体,关于其结构特征,下列说法不正确的是( )| A. | 该几何体是由两个同底的四棱锥组成的几何体 | |
| B. | 该几何体有12条棱、6个顶点 | |
| C. | 该几何体有8个面,并且各面均为三角形 | |
| D. | 该几何体有9个面,其中一个面是四边形,其余均为三角形 |
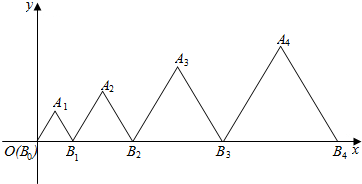 如图,在平面直角坐标系中,边长为an的一组正三角形AnBn-1Bn的底边Bn-1Bn依次排列在x轴上(B0与坐标原点重合).设{an}是首项为a,公差为d的等差数列,若所有正三角形顶点An在第一象限,且均落在抛物线y2=2px(p>0)上,则$\frac{a}{d}$的值为1.
如图,在平面直角坐标系中,边长为an的一组正三角形AnBn-1Bn的底边Bn-1Bn依次排列在x轴上(B0与坐标原点重合).设{an}是首项为a,公差为d的等差数列,若所有正三角形顶点An在第一象限,且均落在抛物线y2=2px(p>0)上,则$\frac{a}{d}$的值为1.