题目内容
16.已知平面内点P(x,y)满足$\left\{\begin{array}{l}{2x+3y≤12}\\{2x+y≥4}\\{y≥0}\end{array}\right.$,O为坐标原点,则目标函数z=$\frac{2y+6}{3x+9}$的取值范围为[$\frac{2}{9}$,$\frac{14}{9}$].分析 作出可行域,z表示区域内的点与D(-3,-3)连线的斜率的三分之二,数形结合可得.
解答 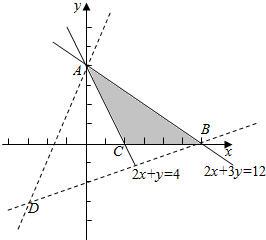 解:作出不等式组$\left\{\begin{array}{l}{2x+3y≤12}\\{2x+y≥4}\\{y≥0}\end{array}\right.$所对应的可行域(如图阴影△ABC),
解:作出不等式组$\left\{\begin{array}{l}{2x+3y≤12}\\{2x+y≥4}\\{y≥0}\end{array}\right.$所对应的可行域(如图阴影△ABC),
z=$\frac{2y+6}{3x+9}$=$\frac{2}{3}$•$\frac{y+3}{x+3}$表示区域内的点与D(-3,-3)连线的斜率的三分之二,
数形结合可得当取区域内的点A(0,4)时,z取最大值$\frac{14}{9}$,
当取区域内的点B(6,0)时,z取最小值$\frac{2}{9}$.
∴目标函数z=$\frac{2y+6}{3x+9}$的取值范围为[$\frac{2}{9}$,$\frac{14}{9}$]
故答案为:[$\frac{2}{9}$,$\frac{14}{9}$].
点评 本题考查简单线性规划,准确作图是解决问题的关键,属中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
11.log${\;}_{\sqrt{2}}$27×log${\;}_{\frac{1}{3}}$8=( )
| A. | 12 | B. | 18 | C. | -18 | D. | -$\frac{9}{2}$ |
 如图,在平行六面体ABCD-A1B1C1D1中,M为AC与D的交点,若$\overrightarrow{{A}_{1}{B}_{1}}$=$\overrightarrow{a}$,$\overrightarrow{A{{\;}_{1}D}_{1}}$=$\overrightarrow{b}$,$\overrightarrow{{A}_{1}A}$=$\overrightarrow{c}$,用基底{$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$}表示向量$\overrightarrow{{C}_{1}M}$.
如图,在平行六面体ABCD-A1B1C1D1中,M为AC与D的交点,若$\overrightarrow{{A}_{1}{B}_{1}}$=$\overrightarrow{a}$,$\overrightarrow{A{{\;}_{1}D}_{1}}$=$\overrightarrow{b}$,$\overrightarrow{{A}_{1}A}$=$\overrightarrow{c}$,用基底{$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$}表示向量$\overrightarrow{{C}_{1}M}$.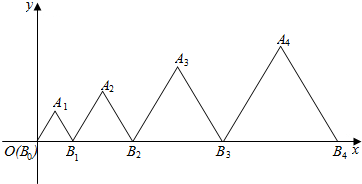 如图,在平面直角坐标系中,边长为an的一组正三角形AnBn-1Bn的底边Bn-1Bn依次排列在x轴上(B0与坐标原点重合).设{an}是首项为a,公差为d的等差数列,若所有正三角形顶点An在第一象限,且均落在抛物线y2=2px(p>0)上,则$\frac{a}{d}$的值为1.
如图,在平面直角坐标系中,边长为an的一组正三角形AnBn-1Bn的底边Bn-1Bn依次排列在x轴上(B0与坐标原点重合).设{an}是首项为a,公差为d的等差数列,若所有正三角形顶点An在第一象限,且均落在抛物线y2=2px(p>0)上,则$\frac{a}{d}$的值为1.