题目内容

已知为f（x）奇函数，在[3，6]上是增函数，[3，6]上的最大值为8，最小值为-1，则2f（-6）+f（-3）等于（　　）
A、-15B、-13C、-5D、5
考点：奇偶性与单调性的综合
专题：函数的性质及应用
分析：f（x）在[3，6]上是增函数，所以f（6）=8，f（3）=-1．而因为f（x）是奇函数，所以2f（-6）+f（-3）=-16+1=-15．
解答： 解：根据已知条件知，f（6）=8，f（3）=-1，f（-6）=-8，f（-3）=1；
∴2f（-6）+f（-3）=-16+1=-15；
故选A．
点评：考查奇函数的定义，以及增函数的定义．
练习册系列答案
相关题目
根据如下样本数据：
x34567
y42.5-1-1-2
得到的线性回归方程为
?
y
=bx+a，则（　　）
A、a＞0，b＞0
B、a＞0，b＜0
C、a＜0，b＞0
D、a＜0，b＜0
已知定义在R上的函数f（x）满足f（x+4）=f（x）+2f（2），若函数y=f（x-1）的图象关于直线x=1对称，且f（3）=2，则f（2015）等于（　　）
A、2B、3C、4D、6
已知函数f（x）=
|lgx|，0＜x≤10
-
1
2
x+6，x＞10
．
（1）若a＜b＜10，且f（a）=f（b），求ab的值；
（2）方程f（x）=k，k为常数，若方程有三解，求k的范围．
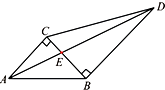如图，两块直角三角板拼在一起，已知∠ABC=45°，∠BCD=60°．若记
AB
=
a
，
AC
=
b
，试用
a
，
b
表示向量
CD
=
 
．
设点（a，b）是区域
x+y-4≤0
x＞0
y＞0
内的随机点，函数f（x）=ax2-4bx+1在区间[1，+∞）是增函数的概率为
 
．
若定义在区间[-2014，2014]上的函数，f（x）满足：对于任意的x1，x2∈[-2014，2014]，都有f（x1+x2）=f（x1）+f（x2）-2012，且x＞0时，有f（x）＞2012，若f（x）的最大值、最小值分别为M，N，则M+N的值为（　　）
A、4024B、2013
C、2012D、4026
设变量x，y满足约束条件
x-y≥-1
x+y≤4
y≥2
，则函数z=2x+4y的最小值为
 
．
已知a＞0且a≠1，则函数f（x）=ax+2+1的图象过定点
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网