题目内容
已知f（x）=x2+2x+4（x∈[-2，2]）则f（x）的值域为 ．
考点：二次函数在闭区间上的最值
专题：函数的性质及应用
分析：运用二次函数的性质得出[-2，-1]单调递减，[-1，2]单调递增，求出f（-2）=4，f（-1）=3，f（2）=12，判断最大值，最小值，即可得到值域．
解答：
解：∵f（x）=x2+2x+4（x∈[-2，2]）
∴对称轴x=-1，
∴f（-2）=4，f（-1）=3，f（2）=12
∴f（x）的值域为[3，12]
故答案为：[3，12]
∴对称轴x=-1，
∴f（-2）=4，f（-1）=3，f（2）=12
∴f（x）的值域为[3，12]
故答案为：[3，12]
点评：本题考察了二次函数的性质，运用求解值域．
练习册系列答案
相关题目
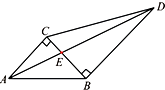如图，两块直角三角板拼在一起，已知∠ABC=45°，∠BCD=60°．若记