题目内容
已知函数f(x)=x2+ax+b,x∈(-1,3),f(x)≤0恒成立,则2a+b的取值范围为 .
考点:二次函数的性质
专题:函数的性质及应用
分析:由题意可得
,变形求得2a+b的取值范围.
|
解答:
解:由题意可得
,∴-a+b≤-1,9a+3b≤-27.
再把这两个式子相加可得 8a+4b≤-28,∴2a+b≤-7,
故答案为:(-∞,-7].
|
再把这两个式子相加可得 8a+4b≤-28,∴2a+b≤-7,
故答案为:(-∞,-7].
点评:本题主要考查二次函数的性质,函数的恒成立问题,体现了转化的数学思想,属于基础题.

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案
相关题目
给出下列四个命题,其中假命题是( )
| A、样本方差反映了样本数据与样本平均值的偏离程度 | ||
| B、从匀速传递的新产品生产流水线上,质检员每10分钟从中抽取一件新产品进行某项指标检测,这样的抽样是分层抽样 | ||
| C、在回归分析模型中,残差平方和越小,说明模型的拟合效果越好 | ||
D、设随机变量X服从正态分布N(0,1),若P(x>1)=p,则P(-1<x<0)=
|
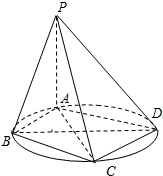 (文)如图,四棱锥P-ABCD的底面ABCD是圆内接四边形(记此圆为W),且PA⊥平面ABCD.
(文)如图,四棱锥P-ABCD的底面ABCD是圆内接四边形(记此圆为W),且PA⊥平面ABCD.