题目内容
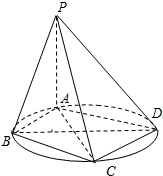 (文)如图,四棱锥P-ABCD的底面ABCD是圆内接四边形(记此圆为W),且PA⊥平面ABCD.
(文)如图,四棱锥P-ABCD的底面ABCD是圆内接四边形(记此圆为W),且PA⊥平面ABCD. (1)当AC是圆W的直径时,求证:平面PBC⊥平面PAB;
(2)当BD是圆W的直径时,PA=BD=2,AD=CD=
| 3 |
(3)在(2)的条件下,证明:直线AB不可能与平面PCD平行.
考点:棱柱、棱锥、棱台的体积,平面与平面垂直的判定
专题:综合题,空间位置关系与距离
分析:(1)应用面面垂直的判定定理,证得BC⊥平面PAB即可;
(2)求出S△ABD=S△BCD=
,即可求出四棱锥P-ABCD的体积;
(3)利用反证法进行证明即可.
(2)求出S△ABD=S△BCD=
| ||
| 2 |
(3)利用反证法进行证明即可.
解答:
(1)证明:∵AC是圆的直径,∴AB⊥CB,
∵PA⊥平面ABCD,∴PA⊥BC,
∴BC⊥平面PAB,
又BC?平面PBC,
∴平面PBC⊥平面PAB;
(2)解:∵BD是圆W的直径时,BD=2,AD=CD=
,
∴AB=BC=1,
∴S△ABD=S△BCD=
.
∵PA=2,
∴四棱锥P-ABCD的体积为
•
•2=
;
(3)证明:假设直线AB与平面PCD平行,则AB∥CD,
由(2)知∠ABC=30°,∠CDB=60°,
∴AB与CD不平行,
∴直线AB不可能与平面PCD平行.
∵PA⊥平面ABCD,∴PA⊥BC,
∴BC⊥平面PAB,
又BC?平面PBC,
∴平面PBC⊥平面PAB;
(2)解:∵BD是圆W的直径时,BD=2,AD=CD=
| 3 |
∴AB=BC=1,
∴S△ABD=S△BCD=
| ||
| 2 |
∵PA=2,
∴四棱锥P-ABCD的体积为
| 1 |
| 3 |
| 3 |
2
| ||
| 3 |
(3)证明:假设直线AB与平面PCD平行,则AB∥CD,
由(2)知∠ABC=30°,∠CDB=60°,
∴AB与CD不平行,
∴直线AB不可能与平面PCD平行.
点评:本题主要考查空间直线与平面的位置关系,考查面面垂直、线面平行的判定与性质,同时考查四棱锥P-ABCD的体积的求法,是一道综合题.

练习册系列答案
 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案 高效智能课时作业系列答案
高效智能课时作业系列答案
相关题目
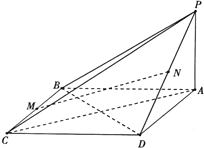 在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为菱形,M,N分别是BC和PD的中点.
在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为菱形,M,N分别是BC和PD的中点.