题目内容
已知函数f(x)=
x3+ax2+6x的单调递减区间是[2,3],则实数a= .
| 1 |
| 3 |
考点:利用导数研究函数的单调性
专题:导数的概念及应用
分析:由f′(x)=x2+2ax+6,判断知△=4a2-24>0,得a>
,a<-
,由函数f(x)=
x3+ax2+6x的单调递减区间是[2,3],则f′(x)=x2+2ax+6=0的根为2和3,则-2a=2+3,得a=-
.
| 6 |
| 6 |
| 1 |
| 3 |
| 5 |
| 2 |
解答:
解:函数的导数为f′(x)=x2+2ax+6,
判断知△=4a2-24>0,得a>
,a<-
,
由函数f(x)=
x3+ax2+6x的单调递减区间是[2,3],
则f′(x)=x2+2ax+6=0的根为2和3,则-2a=2+3,得a=-
,
故答案为:-
.
判断知△=4a2-24>0,得a>
| 6 |
| 6 |
由函数f(x)=
| 1 |
| 3 |
则f′(x)=x2+2ax+6=0的根为2和3,则-2a=2+3,得a=-
| 5 |
| 2 |
故答案为:-
| 5 |
| 2 |
点评:本题考察了函数的单调性,二次函数的性质,是一道基础题.

练习册系列答案
相关题目
函数y=
的单调递减区间是( )
| lnx |
| x |
| A、(e-1,+∞) |
| B、(0,e-1) |
| C、(-∞,e-1) |
| D、(e,+∞) |
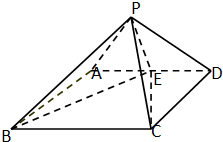 如图,四棱锥P-ABCD的底面是矩形,侧面PAD⊥底面ABCD,在△PAD中
如图,四棱锥P-ABCD的底面是矩形,侧面PAD⊥底面ABCD,在△PAD中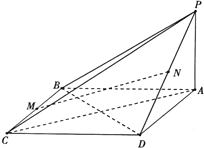 在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为菱形,M,N分别是BC和PD的中点.
在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为菱形,M,N分别是BC和PD的中点. 如图,在底面边长为a的正方形的四棱锥P-ABCD中,已知PA⊥平面AC,且PA=a,则直线PB与平面PCD所成的角大小为
如图,在底面边长为a的正方形的四棱锥P-ABCD中,已知PA⊥平面AC,且PA=a,则直线PB与平面PCD所成的角大小为