题目内容
设F1,F2是椭圆
+
=1(a>b>0)的两个焦点,P为椭圆上任意一点,当∠F1PF2取最大值时的余弦值为-
,则椭圆的离心率为 .
| x2 |
| a2 |
| y2 |
| b2 |
| 1 |
| 49 |
考点:椭圆的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:根据椭圆的性质可得,当P是椭圆短轴的顶点时,∠F1PF2 取最大值,利用条件,即可求出椭圆的离心率
解答:
解:根据椭圆的性质可得,当P是椭圆短轴的顶点时,∠F1PF2 取最大值,
∵P为椭圆上任意一点,当∠F1PF2取最大值时的余弦值为-
,
∴
-1=-
,
∴
=
,
∴
=
.
故答案为:
.
∵P为椭圆上任意一点,当∠F1PF2取最大值时的余弦值为-
| 1 |
| 49 |
∴
| 2b2 |
| a2 |
| 1 |
| 49 |
∴
| b |
| a |
2
| ||
| 7 |
∴
| c |
| a |
| 5 |
| 7 |
故答案为:
| 5 |
| 7 |
点评:本题考查椭圆的标准方程,以及简单性质的应用,考查计算能力,比较基础.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目
函数y=
的单调递减区间是( )
| lnx |
| x |
| A、(e-1,+∞) |
| B、(0,e-1) |
| C、(-∞,e-1) |
| D、(e,+∞) |
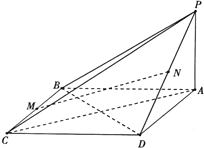 在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为菱形,M,N分别是BC和PD的中点.
在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为菱形,M,N分别是BC和PD的中点.