题目内容
已知不等式|2x-4|-1＜x
（Ⅰ）求该不等式的解集M；
（Ⅱ）若a∈M，求证：
-
＜
-
．
（Ⅰ）求该不等式的解集M；
（Ⅱ）若a∈M，求证：
| a+1 |
| a |
| a |
| a-1 |
考点：绝对值不等式的解法
专题：不等式的解法及应用
分析：（I）不等式即|2x-4|＜1+x，可得
，由此求得不等式的解集M．
（II）由条件求得1＜a＜5，
-
＞0，
-
＞0．再根据
=
＜1，可得要证的不等式成立．
|
（II）由条件求得1＜a＜5，
| a+1 |
| a |
| a |
| a-1 |
| ||||
|
| ||||
|
解答：
解：（I）不等式即|2x-4|＜1+x，
∴
，解得 1＜x＜5，
∴不等式的解集M=（1，5）．
（II）∵a∈M，∴1＜a＜5，∴
-
＞0，
-
＞0．
再根据
=
＜1，
∴
-
＜
-
成立．
∴
|
∴不等式的解集M=（1，5）．
（II）∵a∈M，∴1＜a＜5，∴
| a+1 |
| a |
| a |
| a-1 |
再根据
| ||||
|
| ||||
|
∴
| a+1 |
| a |
| a |
| a-1 |
点评：本题主要考查绝对值不等式的解法，体现了转化、分类讨论的数学思想，属于基础题．
练习册系列答案
相关题目
下列命题正确的是（ ）
| A、a∥b，a⊥α⇒a⊥b |
| B、a⊥α，b⊥α⇒a∥b |
| C、a⊥α，a⊥b⇒b∥α |
| D、a∥α，a⊥b⇒b⊥α |
如图，四棱锥P-ABCD中，底面ABCD是矩形，PA=AB=1，AD=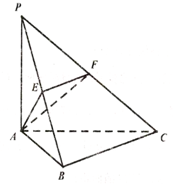
如图，在三棱锥P-ABC中，∠ABC=90°，PA⊥平面ABC，E，F分别为PB，PC的中点．
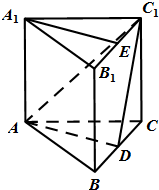如图，正三棱柱ABC-A1B1C1的侧棱为2，底面是边长为2的等边三角形，D，E分别是线段BC，B1C1的中点．