题目内容
 如图,四棱锥P-ABCD中,底面ABCD是矩形,PA=AB=1,AD=
如图,四棱锥P-ABCD中,底面ABCD是矩形,PA=AB=1,AD=| 3 |
| 5 |
(Ⅰ)点E为BC的中点时,试判断PC与平面AEF的位置关系,并说明理由;
(Ⅱ)求证:无论点E在BC边的何处,都有PE⊥AF;
(Ⅲ)当BE为何值时,PA与平面PDE所成角的大小为45°?
考点:直线与平面所成的角,空间中直线与平面之间的位置关系
专题:综合题,空间位置关系与距离,空间角
分析:(Ⅰ)利用勾股定理证明PA⊥平面ABCD,建立空间直角坐标系,证明
=(-
,-1,1)=
,即可证明PC∥平面AEF;
(II)证明
•
=0即可;
(Ⅲ)求出平面PDE的一个法向量,利用PA与平面PDE所成角为45°,可得sin45°=
=
,即可求出结论.
| CP |
| 3 |
| 1 |
| 2 |
| EF |
(II)证明
| PE |
| AF |
(Ⅲ)求出平面PDE的一个法向量,利用PA与平面PDE所成角为45°,可得sin45°=
| ||
| 2 |
| ||||
|
解答:
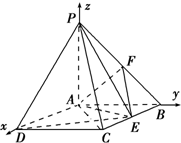 (Ⅰ)解:∵PA=AB=1,AD=
(Ⅰ)解:∵PA=AB=1,AD=
,PC=
,PD=2,
∴PA2+AD2=PD2,PA2+AC2=PA2+AD2+DC2=PC2,
∴PA⊥AD,PA⊥AC
∵AD∩AC=A,
∴PA⊥平面ABCD
分别以
,
,
为Ox轴,Oy轴,Oz轴,建立空间直角坐标系,如图所示,则B(0,1,0),C(
,1,0),D(
,0,0),P(0,0,1),F(0,
,
).
当点E为BC的中点时,E(
,1,0)
∴
=(-
,-
,
)
又
=(-
,-1,1)=
∴CP∥EF.
又PC?平面AEF,而EF?平面AEF,
∴PC∥平面AEF.
(II)证明:设BE=a(0≤a≤
),则E(a,1,0),
•
=(a,1,-1)•(0,
,
)=0,
∴PE⊥AF.
(III)解:设
=(x,y,z)是平面PDE的一个法向量,
由
,取
=(1,
-a,
).
而
=(0,0,1),依题意PA与平面PDE所成角为45°,
∴sin45°=
=
,
得BE=a=
-
或BE=a=
+
>
(舍去).
故BE=
-
时,PA与平面PDE所成角为45°.
 (Ⅰ)解:∵PA=AB=1,AD=
(Ⅰ)解:∵PA=AB=1,AD=| 3 |
| 5 |
∴PA2+AD2=PD2,PA2+AC2=PA2+AD2+DC2=PC2,
∴PA⊥AD,PA⊥AC
∵AD∩AC=A,
∴PA⊥平面ABCD
分别以
| AD |
| AB |
| AP |
| 3 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
当点E为BC的中点时,E(
| ||
| 2 |
∴
| EF |
| ||
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
又
| CP |
| 3 |
| 1 |
| 2 |
| EF |
∴CP∥EF.
又PC?平面AEF,而EF?平面AEF,
∴PC∥平面AEF.
(II)证明:设BE=a(0≤a≤
| 3 |
| PE |
| AF |
| 1 |
| 2 |
| 1 |
| 2 |
∴PE⊥AF.
(III)解:设
| n |
由
|
| n |
| 3 |
| 3 |
而
| AP |
∴sin45°=
| ||
| 2 |
| ||||
|
得BE=a=
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
故BE=
| 3 |
| 2 |
点评:本题考查直线与平面平行的判定,异面直线垂直判定、异面直线所成角的求法,在适合建立空间坐标系的情况下,转化为用空间坐标系中的向量法解决,较为简捷.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
已知F1,F2分别是双曲线C:
-
=1的左、右两个焦点.若C上存在一点P,使得|
|•|
|=2a2,则C的离心率e的取值范围是( )
| x2 |
| a2 |
| y2 |
| b2 |
| PF1 |
| PF2 |
A、(1,
| ||
B、[
| ||
C、(1,
| ||
D、[
|
 如图,在梯形ABCD中,AD⊥CD,AD∥CD,AD=CD=
如图,在梯形ABCD中,AD⊥CD,AD∥CD,AD=CD=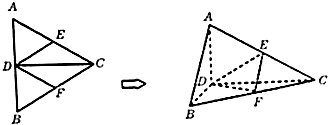
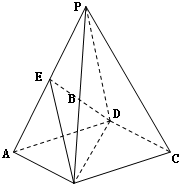 如图,在四棱柱P-ABCD中,底面ABCD是矩形,E是棱PA的中点,PD⊥BC.求证:
如图,在四棱柱P-ABCD中,底面ABCD是矩形,E是棱PA的中点,PD⊥BC.求证: