题目内容
设函数f(x)=(
-1)2+(
-1)2,其中x∈(0,+∞),设t=
+
(1)当a=1,b=4时,用t表示f(x),并求出f(x)的最小值;
(2)设k>0,当a=k2,b=(k+1)2时,若1≤f(x)≤9对任意x∈[a,b]恒成立,求k的取值范围.
| x |
| a |
| b |
| x |
| x |
| a |
| b |
| x |
(1)当a=1,b=4时,用t表示f(x),并求出f(x)的最小值;
(2)设k>0,当a=k2,b=(k+1)2时,若1≤f(x)≤9对任意x∈[a,b]恒成立,求k的取值范围.
考点:利用导数求闭区间上函数的最值,利用导数研究函数的单调性
专题:导数的综合应用
分析:(1)利用基本不等式可得t的取值范围,通过配方和利用乘法公式即可得出f(x)用t表示的表达式,再利用二次函数的单调性即可得出;
(2)利用导数可得t的取值范围,再利用二次函数的单调性即可得出k的取值范围.
(2)利用导数可得t的取值范围,再利用二次函数的单调性即可得出k的取值范围.
解答:
解:(1)当a=1,b=4时,又x>0,∴t=x+
≥2
=4.当且仅当x=2时取等号.
∴x2+(
)2=(x+
)2-8=t2-8.
∴f(x)=(x-1)2+(
-1)2=x2+(
)2-2(x+
)+2=t2-8-2t+2=t2-2t-6=g(t)
∴g(t)=(t-1)2-7,t∈[4,+∞).
∴当t=4时,g(t)取得最小值2,即x=2时函数f(x)取得最小值2.
(2)∵t=
+
,x∈[a,b].∴t′=
-
=
=
,
令t′=0,解得x=
.
当a≤x<
时,t′<0,此时函数t(x)单调递减;当
<x≤b时,t′>0,此时函数t(x)单调递增.
∴当x=
时,函数t(x)取得最小值,t(
)=2
=
.
又t(a)=t(b)=1+
,∴t∈[
,1+
].
∴f(x)=(
-1)2+(
-1)2=(
+
)2-
-2(
+
)+2=t2-2t+2-
=g(t).t∈[
,1+
].
∵k>0,a=k2,b=(k+1)2,
∴t∈[
,1+
].即t∈[2+
,2+
+
](k>0).
∴g(t)=(t-1)2+1-
=(t-1)2-1-
-
,
当t=2+
时,g(t)取得最小值,g(2+
)≥1;
当t=2+
+
时,g(t)取得最大值,g(2+
+
)≤9.
联立
,化为
,解得1≤k≤
.
∴k的取值范围是[1,
].
| 4 |
| x |
x•
|
∴x2+(
| 4 |
| x |
| 4 |
| x |
∴f(x)=(x-1)2+(
| 4 |
| x |
| 4 |
| x |
| 4 |
| x |
∴g(t)=(t-1)2-7,t∈[4,+∞).
∴当t=4时,g(t)取得最小值2,即x=2时函数f(x)取得最小值2.
(2)∵t=
| x |
| a |
| b |
| x |
| 1 |
| a |
| b |
| x2 |
| x2-ab |
| ax2 |
(x+
| ||||
| ax2 |
令t′=0,解得x=
| ab |
当a≤x<
| ab |
| ab |
∴当x=
| ab |
| ab |
|
2
| ||
| a |
又t(a)=t(b)=1+
| b |
| a |
2
| ||
| a |
| b |
| a |
∴f(x)=(
| x |
| a |
| b |
| x |
| x |
| a |
| b |
| x |
| 2b |
| a |
| x |
| a |
| b |
| x |
| 2b |
| a |
2
| ||
| a |
| b |
| a |
∵k>0,a=k2,b=(k+1)2,
∴t∈[
| 2(k+1) |
| k |
| (k+1)2 |
| k2 |
| 2 |
| k |
| 2 |
| k |
| 1 |
| k2 |
∴g(t)=(t-1)2+1-
| 2b |
| a |
| 4 |
| k |
| 2 |
| k2 |
当t=2+
| 2 |
| k |
| 2 |
| k |
当t=2+
| 2 |
| k |
| 1 |
| k2 |
| 2 |
| k |
| 1 |
| k2 |
联立
|
|
| 2 |
∴k的取值范围是[1,
| 2 |
点评:本题考查了利用导数研究函数的单调性极值与最值、二次函数的单调性,考查了推理能力和计算能力,属于难题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
设集合U={1,2,3,4,5},A={1,3,5},B={2,3,5},则A∪B=( )
| A、U | B、∅ |
| C、{3,5} | D、{1,2,3,5} |
 如图,已知ABCD是空间四边形,AB=AD,CB=CD,求证:BD⊥AC.
如图,已知ABCD是空间四边形,AB=AD,CB=CD,求证:BD⊥AC.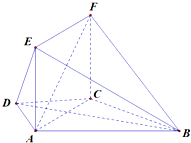 如图,在梯形ABCD中,AD⊥CD,AD∥CD,AD=CD=
如图,在梯形ABCD中,AD⊥CD,AD∥CD,AD=CD= 已知四棱锥P-ABCD的底面为菱形,且∠ABC=60°,AB=PC=2,AP=BP=
已知四棱锥P-ABCD的底面为菱形,且∠ABC=60°,AB=PC=2,AP=BP=