题目内容
已知等比数列{an}的首项为
,公比为-
,设前n项和为Sn,则数列{Sn-
}的最大项的值与最小项的值的比值为 .
| 3 |
| 2 |
| 1 |
| 2 |
| 1 |
| Sn |
考点:等比数列的性质
专题:计算题,等差数列与等比数列
分析:求出Sn,计算数列{Sn-
}的最大项的值与最小项,即可得出比值.
| 1 |
| Sn |
解答:
解:由题意,Sn=
=1-(-
)n=
,
n为奇数时,Sn随着n的增大而减少,所以1<Sn≤S1=
,故0<Sn-
≤
;
n为偶数时,Sn随着n的增大而增大,所以1>Sn≥S2=
,故0>Sn-
≥-
;
所以数列{Sn-
}的最大项的值与最小项的值的比值为
=-
.
故答案为:-
.
| ||||
1+
|
| 1 |
| 2 |
|
n为奇数时,Sn随着n的增大而减少,所以1<Sn≤S1=
| 3 |
| 2 |
| 1 |
| Sn |
| 5 |
| 6 |
n为偶数时,Sn随着n的增大而增大,所以1>Sn≥S2=
| 3 |
| 4 |
| 1 |
| Sn |
| 7 |
| 12 |
所以数列{Sn-
| 1 |
| Sn |
| ||
-
|
| 10 |
| 7 |
故答案为:-
| 10 |
| 7 |
点评:本题考查等比数列的求和公式,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目

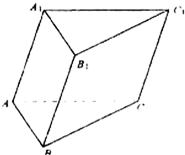 如图,用四种不同颜色给三棱柱ABC-A1B1C1的六个顶点涂色,要求四种颜色全都用上,每个点涂一种颜色,且图中每条线段的两个端点涂不同颜色.则不同的涂色方法的种数为
如图,用四种不同颜色给三棱柱ABC-A1B1C1的六个顶点涂色,要求四种颜色全都用上,每个点涂一种颜色,且图中每条线段的两个端点涂不同颜色.则不同的涂色方法的种数为