题目内容
已知函数f(x)=4cos(ωx-
)sinωx-cos(2ωx+π)(ω>0),其图象与直线y=1的相邻两个交点的距离为π.
(1)若g(x)=f(
x+
),求g(x)在[0,π]上的单调递增区间;
(2)若f(α)+f(
-α)=
,且α∈(
,
),试求
的值.
| π |
| 6 |
(1)若g(x)=f(
| 3 |
| 4 |
| π |
| 4 |
(2)若f(α)+f(
| π |
| 2 |
4+
| ||
| 2 |
| π |
| 4 |
| π |
| 2 |
| (5sin2α+11cos2α-8)(tanα+cotα) | ||||
|
考点:三角函数中的恒等变换应用,同角三角函数基本关系的运用
专题:三角函数的图像与性质
分析:(1)首先,借助于两角和与差的正弦、余弦公式化简,然后,借助于周期公式,确定ω的值,从而得到函数的解析式,最后确定g(x)在[0,π]上的单调递增区间;
(2)根据(1),将等式f(α)+f(
-α)=
化简,然后得到sinα,cosα的差和积的值,最后,对待求式子进行化简,从而得到结果.
(2)根据(1),将等式f(α)+f(
| π |
| 2 |
4+
| ||
| 2 |
解答:
解:(1)∵函数f(x)=4cos(ωx-
)sinωx-cos(2ωx+π),
∴函数f(x)=4(cosωxcos
+sinωxsin
)sinωx+cos2ωx
=
sin2ωx+1-cos2ωx+cos2ωx
=
sin2ωx+1,
∵T=
=2π,
∴ω=
,
∴f(x)=
sinx+1,
∴g(x)=f(
x+
)=
sin(
x+
)+1,
∵x∈[0,π],
∴(
x+
)∈[
,π],
令t=
x+
,
∴y=
sint+1的单调递增区间为[
,
],
∵
≤
x+
≤
,
∴x∈[0,
],
∴g(x)的单调递增区间为[0,
].
(2)根据(1),
(sinα+cosα)+2
∴
(sinα+cosα)+2=
,
∴sinα+cosα=
,
∴cosα-sinα=-
,sinαcosα=
,
∵
=
=
•
=
=
=-4.
∴
的值-4.
| π |
| 6 |
∴函数f(x)=4(cosωxcos
| π |
| 6 |
| π |
| 6 |
=
| 3 |
=
| 3 |
∵T=
| 2π |
| 2ω |
∴ω=
| 1 |
| 2 |
∴f(x)=
| 3 |
∴g(x)=f(
| 3 |
| 4 |
| π |
| 4 |
| 3 |
| 3 |
| 4 |
| π |
| 4 |
∵x∈[0,π],
∴(
| 3 |
| 4 |
| π |
| 4 |
| π |
| 4 |
令t=
| 3 |
| 4 |
| π |
| 4 |
∴y=
| 3 |
| π |
| 4 |
| π |
| 2 |
∵
| π |
| 4 |
| 3 |
| 4 |
| π |
| 4 |
| π |
| 2 |
∴x∈[0,
| π |
| 3 |
∴g(x)的单调递增区间为[0,
| π |
| 3 |
(2)根据(1),
| 3 |
∴
| 3 |
4+
| ||
| 2 |
∴sinα+cosα=
| ||
| 2 |
∴cosα-sinα=-
| 1 |
| 2 |
| 3 |
| 8 |
∵
| (5sin2α+11cos2α-8)(tanα+cotα) | ||||
|
=
(6cos2α-3)(
| ||
| sinα+cosα |
=
| 3(cos2α-sin2α) |
| sinα+cosα |
| 1 |
| sinαcosα |
=
| 3(cosα-sinα) |
| sinαcosα |
3(-
| ||
|
=-4.
∴
| (5sin2α+11cos2α-8)(tanα+cotα) | ||||
|
点评:本题综合考查了二倍角公式、辅助角公式、三角函数的图象与性质、三角恒等变换等知识,考查比较综合,属于中档题.

练习册系列答案
相关题目
若全集U={1,2,3,4,5,6},M={1,4},N={2,3},则集合{5,6}等于( )
| A、M∪N |
| B、M∩N |
| C、(∁UM)∪(∁UN) |
| D、(∁UM)∩(∁UN) |
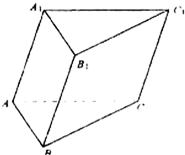 如图,用四种不同颜色给三棱柱ABC-A1B1C1的六个顶点涂色,要求四种颜色全都用上,每个点涂一种颜色,且图中每条线段的两个端点涂不同颜色.则不同的涂色方法的种数为
如图,用四种不同颜色给三棱柱ABC-A1B1C1的六个顶点涂色,要求四种颜色全都用上,每个点涂一种颜色,且图中每条线段的两个端点涂不同颜色.则不同的涂色方法的种数为