题目内容
6.不等式组$\left\{\begin{array}{l}y≤x\\ x+y≤1\\ y≥-1\end{array}\right.$所表示的平面区域的面积为$\frac{9}{4}$.分析 画出满足约束条件$\left\{\begin{array}{l}y≤x\\ x+y≤1\\ y≥-1\end{array}\right.$的可行域,数形结合可得可行域的面积.
解答 解:满足约束条件$\left\{\begin{array}{l}y≤x\\ x+y≤1\\ y≥-1\end{array}\right.$的可行域如下图所示: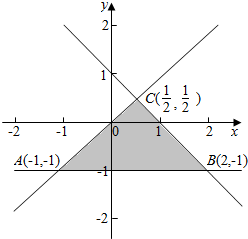
由图可得:可行域是一个底面AB=3,AB边上的高为$\frac{3}{2}$的三角形,
∴可行域的面积S=$\frac{1}{2}$×3×$\frac{3}{2}$=$\frac{9}{4}$,
故答案为:$\frac{9}{4}$.
点评 本题考查的知识点是二元一次不等式(组)与平面区域,正确理解“同正异负”的原则,是解答的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.已知A={2,3,4},B={x||x|<3},则A∩B=( )
| A. | {3} | B. | {2,3} | C. | {2} | D. | {2,3,4} |
14.在△ABC中,a,b,c分别为角A、B、C的对边,若a=2,b=2$\sqrt{3}$,∠A=30°,则∠B等于( )
| A. | 30° | B. | 30°或150° | C. | 60° | D. | 60°或120° |
1.经过两圆x2+y2=9和(x+4)2+(y+3)2=8的交点的直线方程为( )
| A. | 8x+6y+13=0 | B. | 6x-8y+13=0 | C. | 4x+3y+13=0 | D. | 3x+4y+26=0 |
15.函数$f(x)=\sqrt{4-x}+lg\frac{{{x^2}-5x+6}}{x-3}$的定义域为( )
| A. | (2,3) | B. | (2,4) | C. | (2,3)∪(3,4] | D. | (-1,3)∪(3,6] |
16.下列四组函数中,表示相等函数的一组是( )
| A. | $f(x)=x,g(x)=\sqrt{x^2}$ | B. | f(x)=x,g(x)=|x| | C. | f(x)=x2-1,g(t)=t2-1 | D. | $f(x)=x,g(x)={(\sqrt{x})^2}$ |